[ 기말 범위 ]
- 확률 & 확률변수
- 분포 (이산형, 연속형)
- 기댓값 (분산, 표준편차)
[2학기 통계학2에서는 ?]
- 선형대수 개념 → AI (머신러닝)
- 고윳값, 고유벡터
- 분산(공분산) → 상관계수, 회귀분석
- 주성분 분석(PCA), SVA

베이지안 모델
- 불확실성을 확률분포로 나타내고, 이를 데이터와 결합하여 모델링하는 방법
- 모델의 불확실성을 사전분포로 나타낸다.
- 데이터를 통해 사후분포를 계산할 수 있다.
- 사후분포 = 사전분포와 데이터를 결합한 분포

★ 베이지안 통계학 ★
- 기존의 불확실성을 최대한 줄이고, 더 정확한 결론을 도출할 수 있게 된다.
- 가지고 있는 정보 : 사전확률, 시도 결과 : 사후확률
- 이전의 확률에 새로운 정보를 반영하여 더 정확한 결과를 얻게 되는 것이다.

빈도확률론 VS 베이즈확률론
- 빈도확률론은 장기적으로 반복되는 동일한 상황에서, 즉 무한한 공간에서 어떤 사건이 일어날 확률을 계산하는 것
- 베이즈확률론은 사전 정보와 현재 관측된 데이터를 결합하여 어떤 사건이 일어날 확률을 계산하는 것이다.


베이지안 통계학이 왜 중요한가?
- 첫째로, 베이지안 통계학은 불확실성을 다루기에 더 적합하다. 사건의 가능성을 단순히 다루는 것이 아닌, 사전의 사건결과에 데이터를 결합시켜 예측이나 의사결정을 할 수 있다. 집단에는 패턴이 있다. 이것은 분포를 띄우고, 그 안에는 데이터가 들어있다.
- 둘째로, 베이지안 통계학은 모형의 복잡도를 다루기에 더 적합하다.

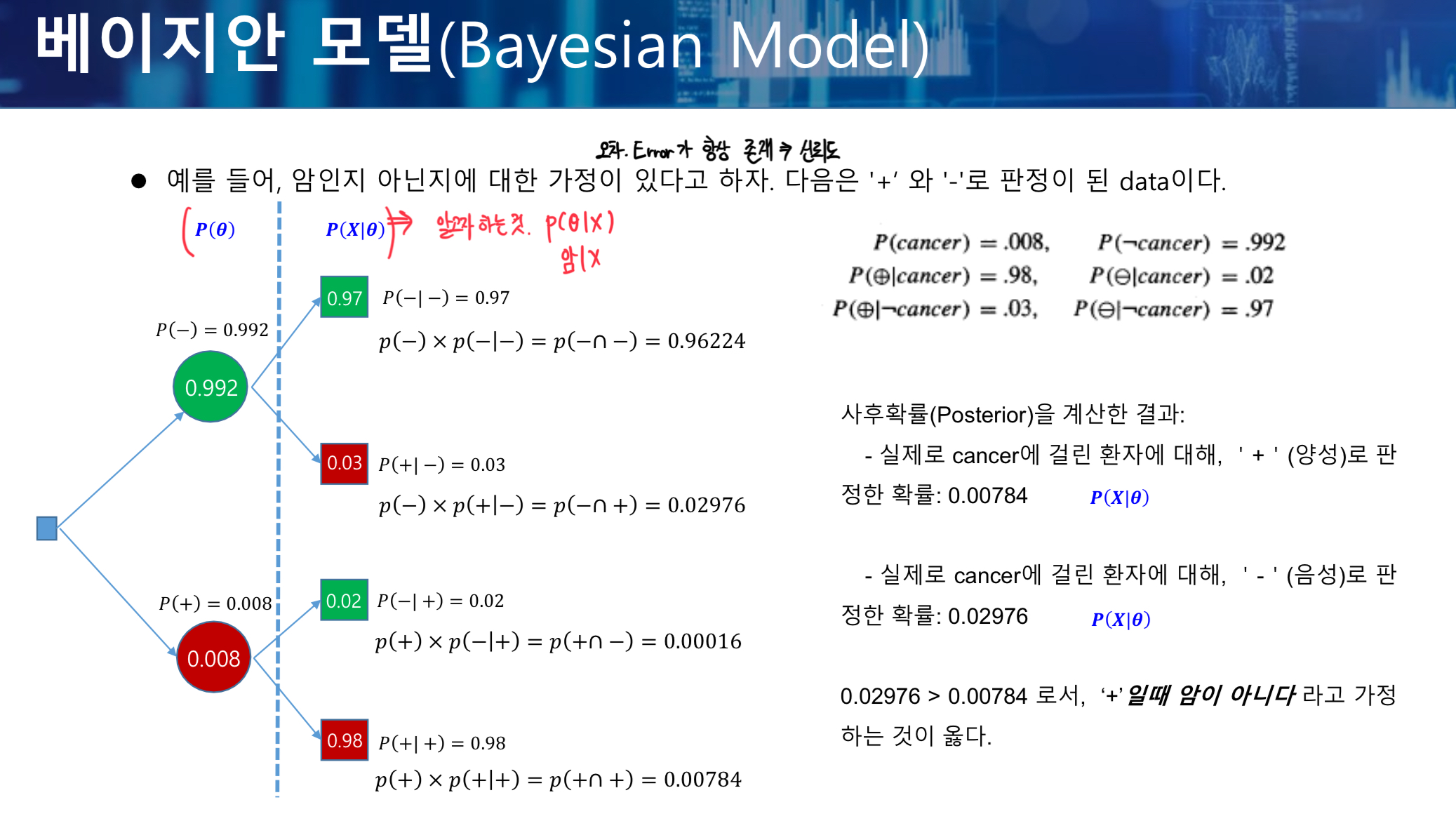
- 오차, Error값은 항상 존재한다. 그리고 오차가 작을수록 신뢰도가 높다는 것을 의미한다.

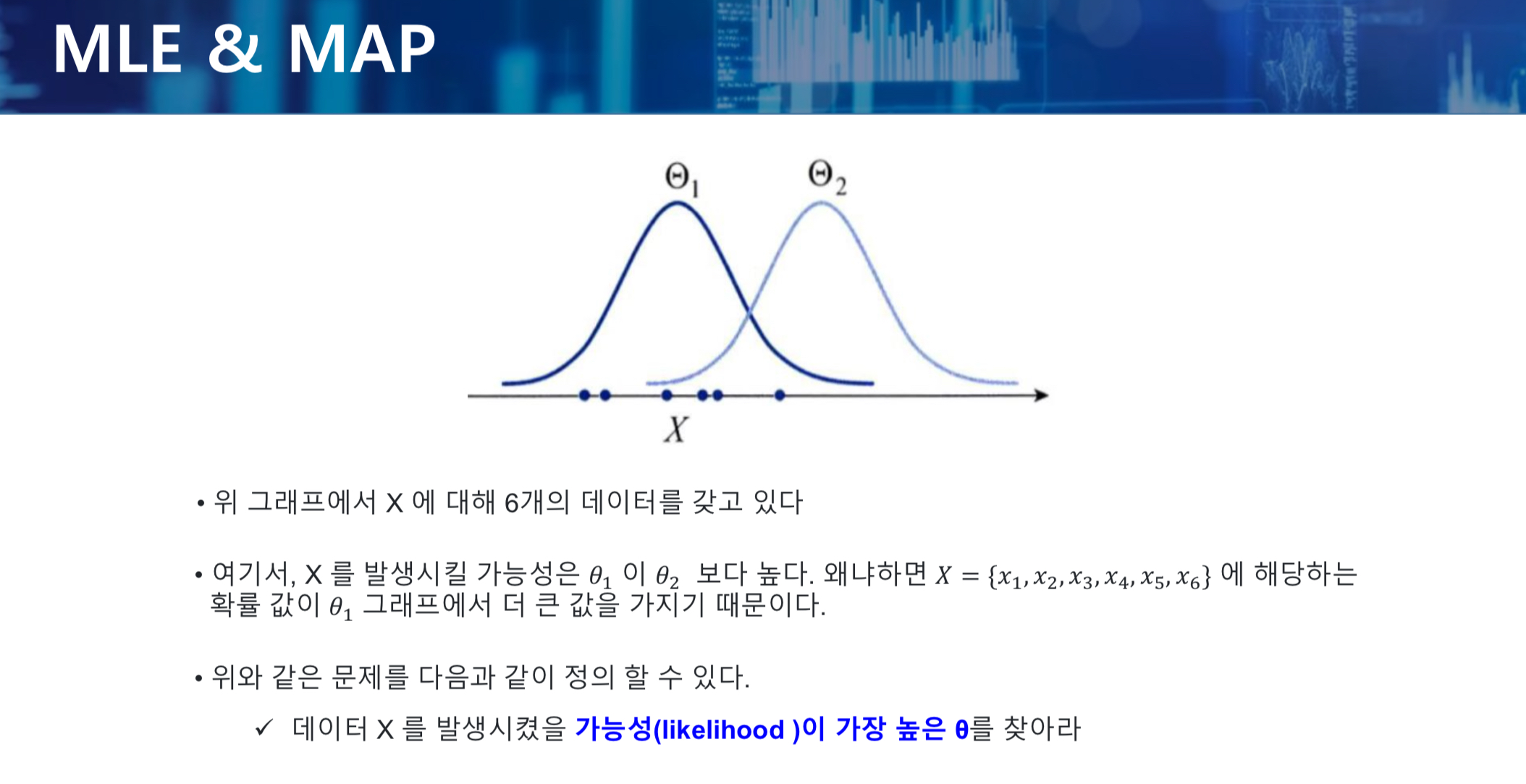
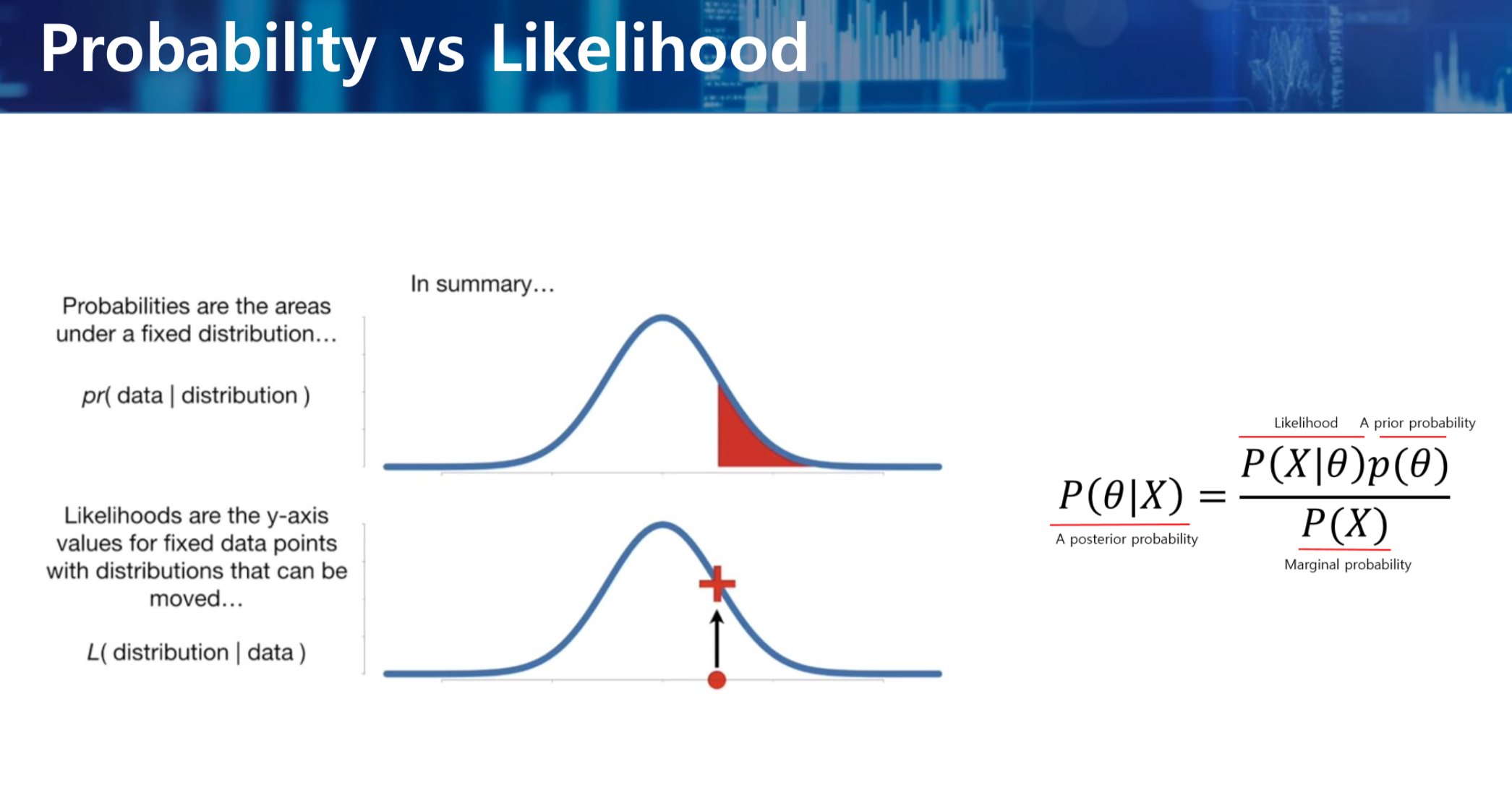
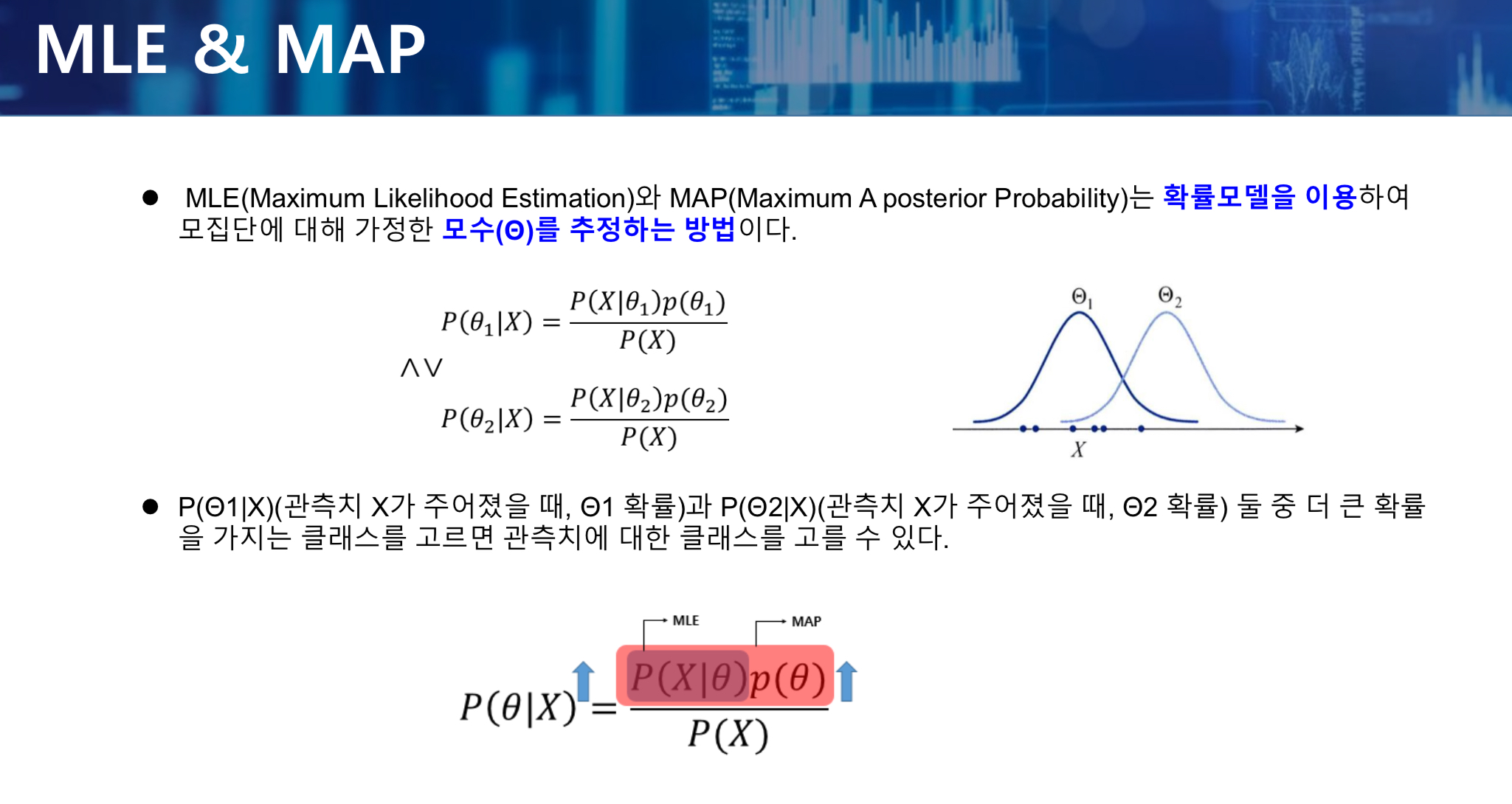

- P(X) : 이미 (사전) 결과이므로 조작의 대상이 아니다.
- P(X | Q) * P(Q) 전체를 최대로 하는 것이 곧 사후확률을 최대화하는 것이며, 이 방법을 MAP이라고 한다.
[수업때 다루지 않음, 참고만]





'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (10) (1) | 2024.06.17 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (9) (1) | 2024.06.17 |
| 머신 러닝을 위한 통계학 필기 (7) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (6) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (5) (0) | 2024.04.18 |