[저번 수업 복습]
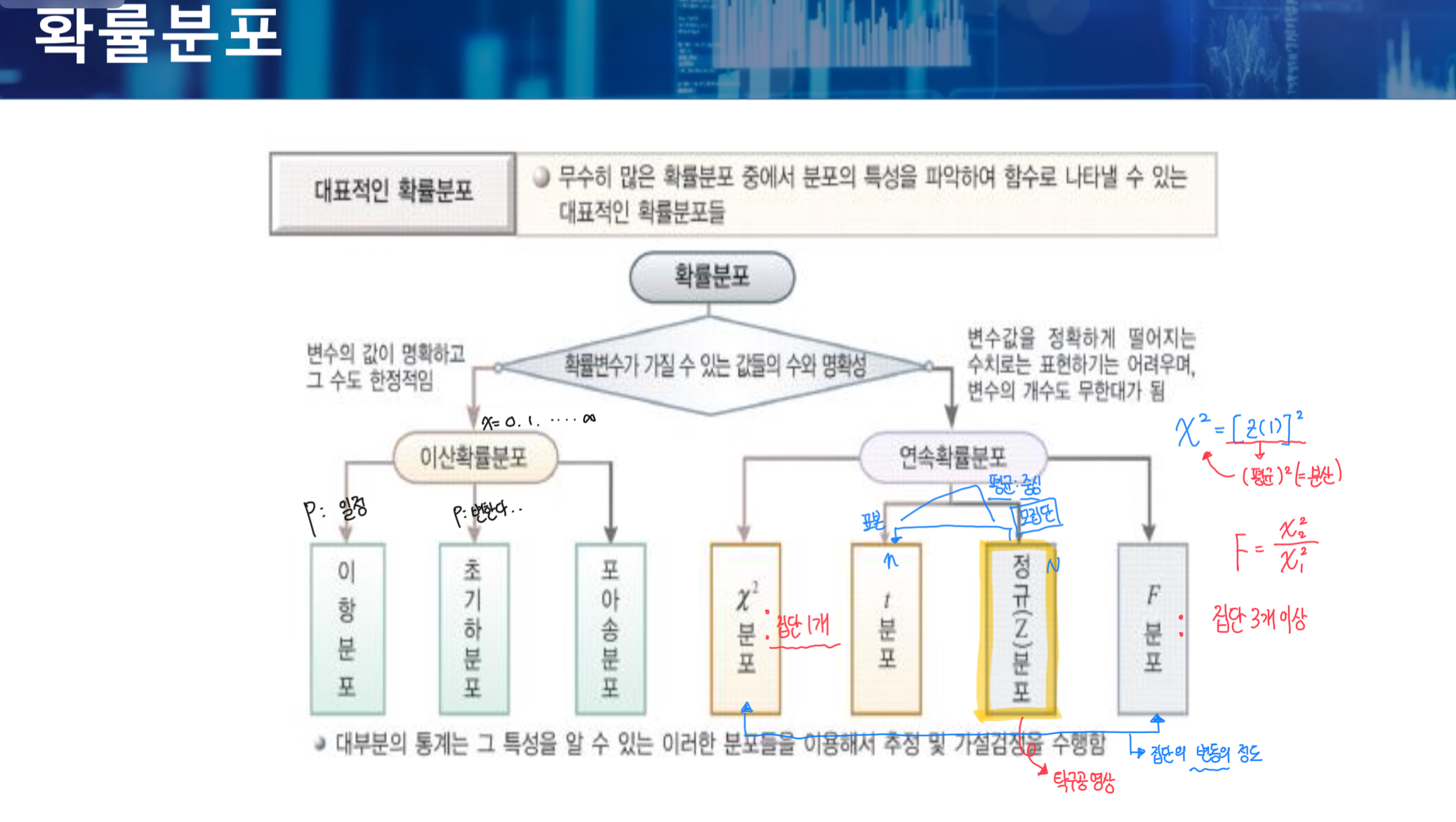
이항분포 VS 초기하분포 (헷갈림 주의)
- 이항분포는 확률p가 일정하다.
- 초기하분포는 확률p가 변한다.
- 이항분포는 애초에 기대값, 분산을 구하려면 (np 또는 npq) 문제에서 확률의 개념이 주어진다.
- 반면에, 초기하 분포는 총 개수 중 불량품의 개수가 몇 개인데, 임의로 몇 개를 택한다와 같은 유형의 문제가 다수이다.
카이제곱 분포 & F분포
- 카이제곱 분포와 F분포는 집단의 변동의 정도를 사용한다. (변동성)
- F분포는 집단 여러 개를 대상으로 한다. F는 분산 제곱끼리의 비를 의미한다.

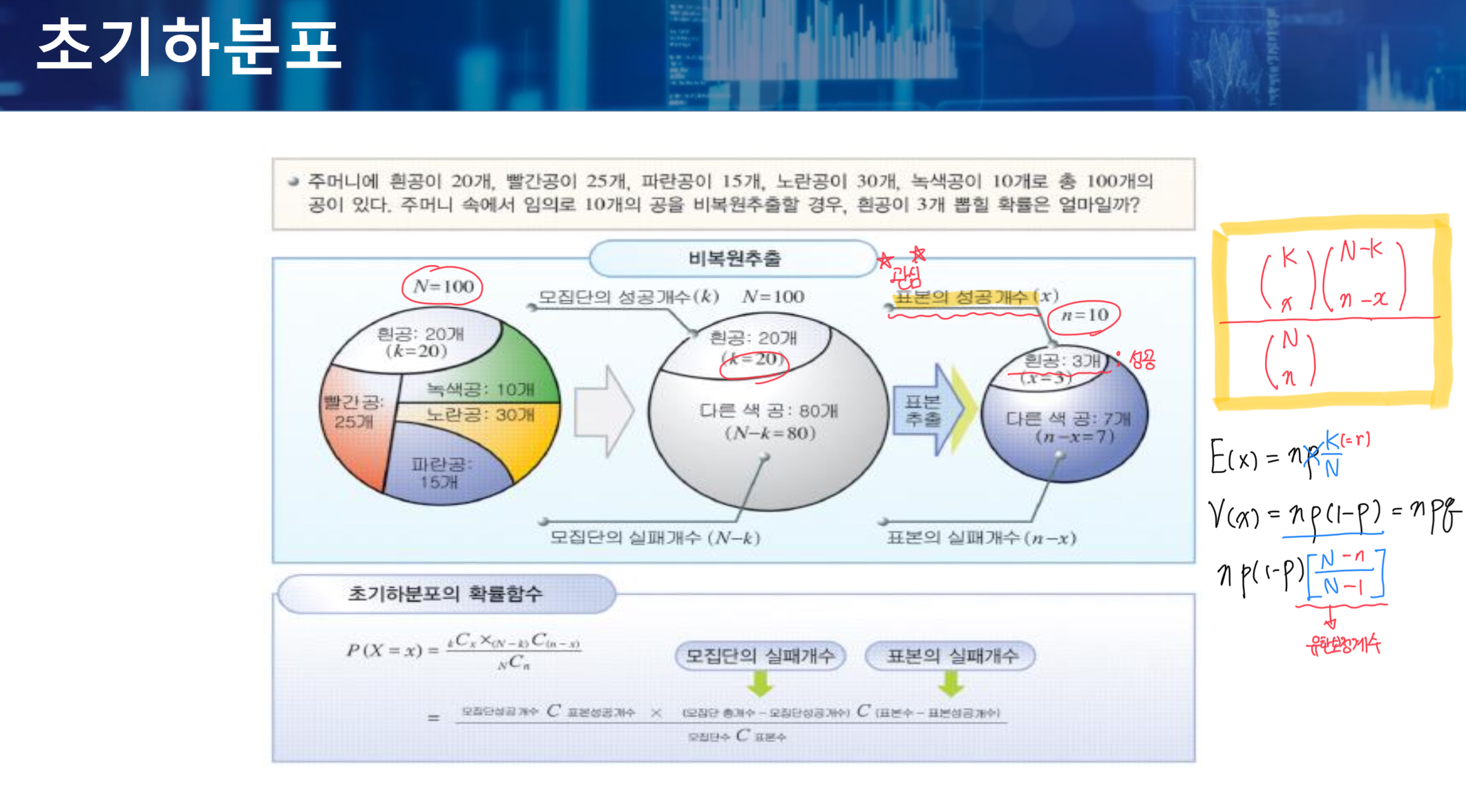
초기하분포의 관심은 표본의 성공개수이다. + 비복원추출



포아송분포
- 일정한 단위시간과 거리 혹은 면적 등에서 발생하는 관심있는 사건의 횟수를 변수값으로 하는 확률변수의 확률분포를 말한다.
- 포아송분포하는 확률변수 예시의 특징으로는 최대 얼마인지 모르는 경우이다.




[연속확률분포]

정규분포 (Z)
- 연속확률분포 중에 가장 대표적인 분포
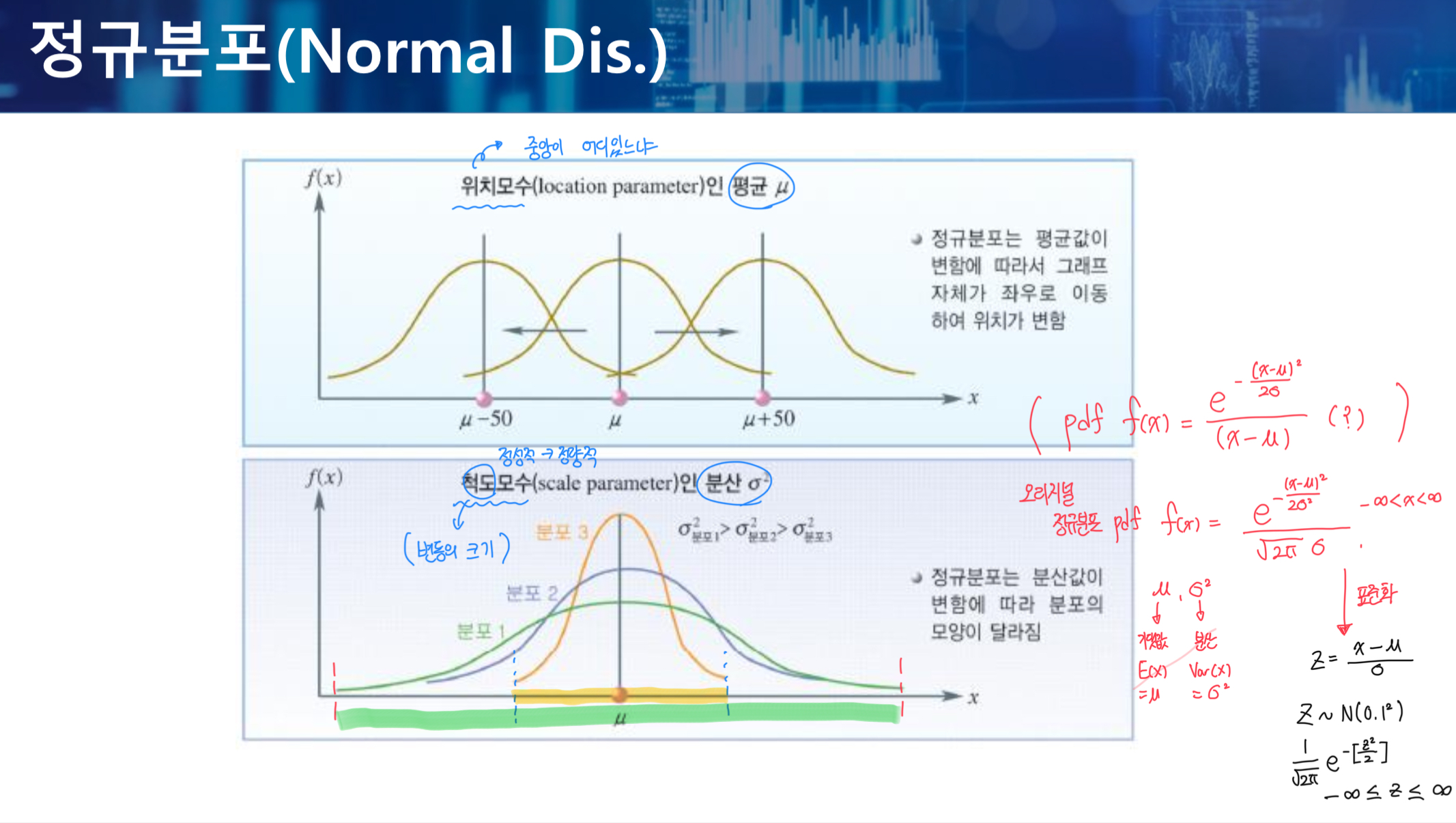
- 종모양으로 좌우대칭인 분포
- 평균과 분산에 따라 구체적인 분포의 위치와 모양이 결정된다.
- 평균을 중심으로 종모양의 좌우대칭인 분포
- 확률밀도함수 곡선과 X축 사이의 전체 면적의 합은 1이 된다.
- 종모양의 중앙이 볼록할수록, 정규분포에 더 가까워진다.
Q. 집단의 특성을 파악하는 통계량은? (2개)
- 평균(중앙 및 중심파악)과 편차(변동성 파악)
Q. 변동성이 큰 집단과 변동성이 작은 집단을 통계적으로 해석할 때, 신뢰도 차이가 있는가?
- 있다, 변동성이 큰 집단일수록 신뢰도는 떨어지고 변동성이 작은 집단일수록 신뢰도는 올라간다.
- 그 이유는, 오차가 줄어들고 예시로는 양궁 과녁의 정확도가 있다.
확률VS통계
- 확률은 하나의 사건에 대한 것이고, 통계는 사건이 합쳐진 집단을 의미한다.
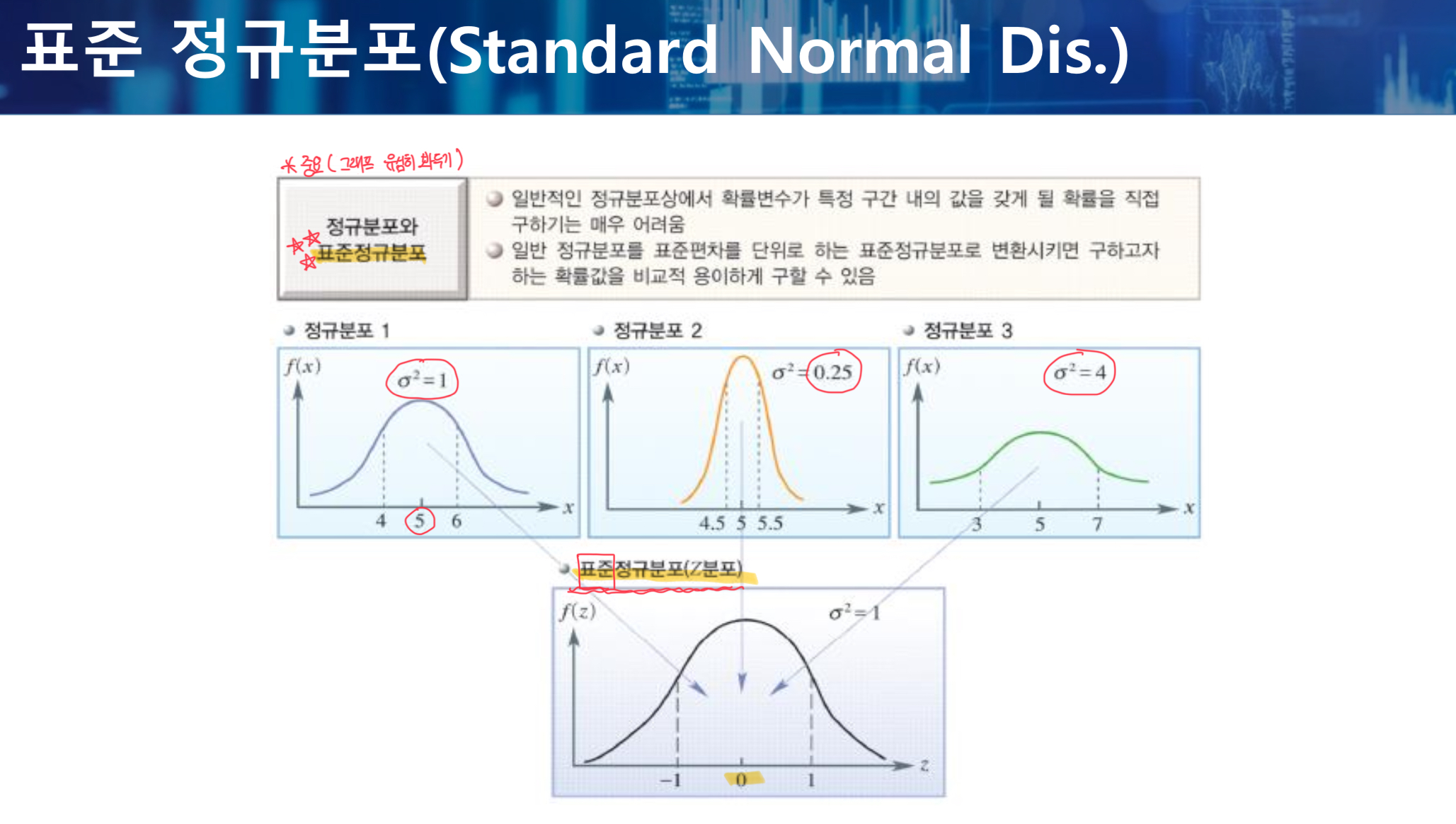
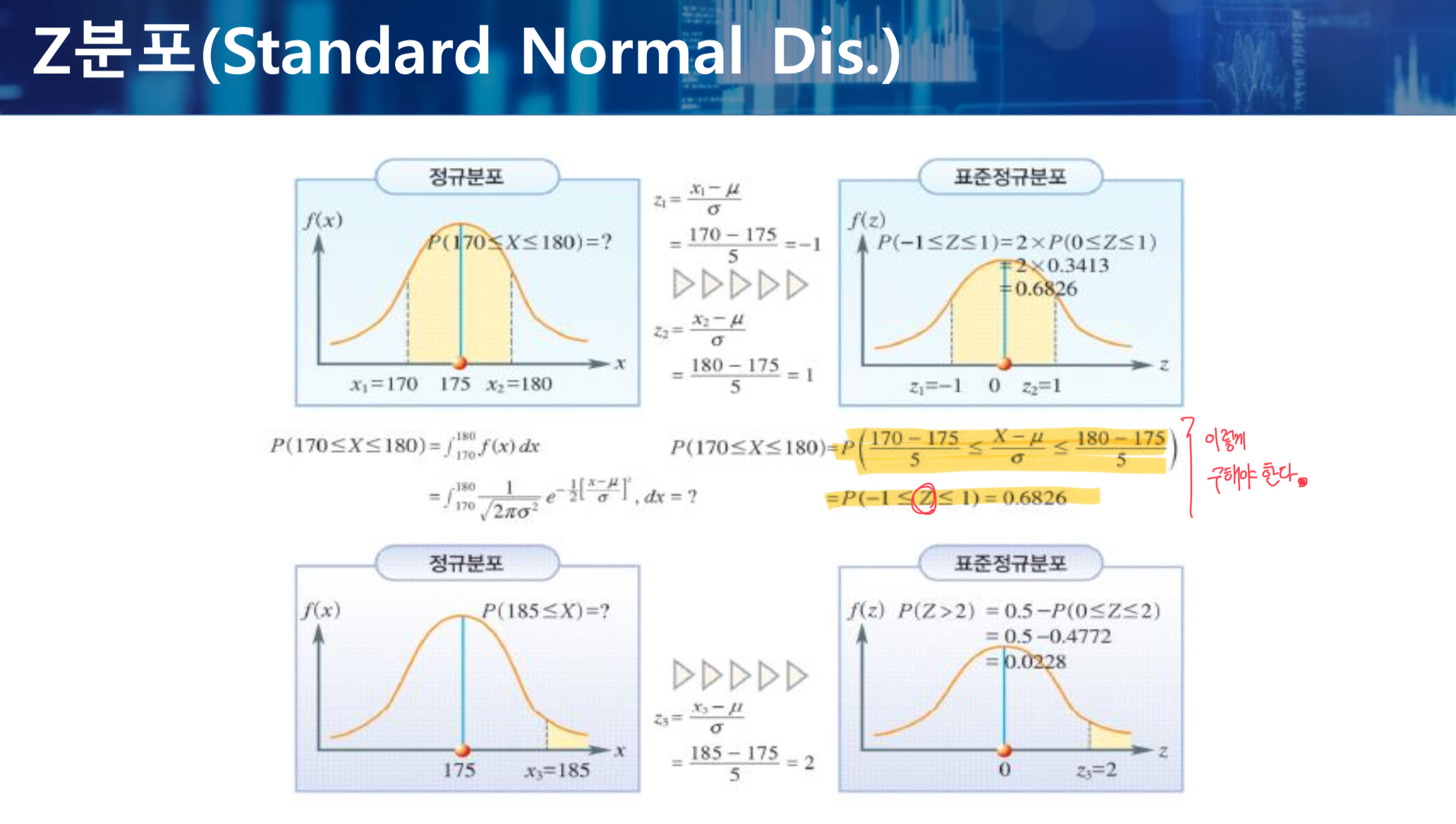
정규분포를 표준화시켜 표준정규분포로 변환시키면, 구하고자 하는 확률값을 비교적 용이하게 구할 수 있다.
표준정규분포는 평균이 0이고, 분산이 1인 분포를 말한다.


표준정규분포 (Z분포)
- 정규분포하는 확률변수 X를 표준화한 값을 변수값으로 하는 확률변수 Z의 분포

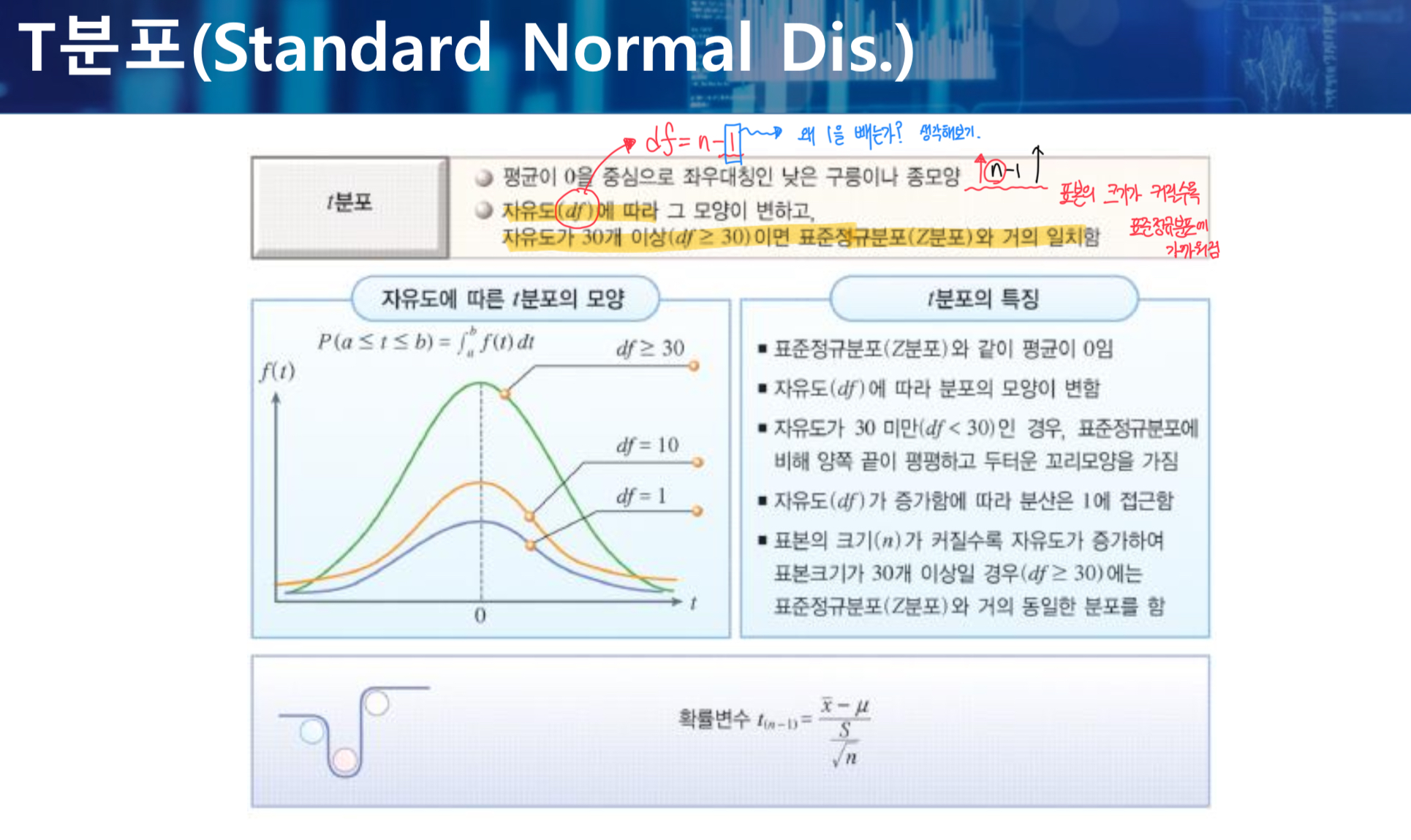
t분포
- 자유도(df)에 따라 그 모양이 변하고, 표본의 개수가 30개 미만이여야 한다.
- 그 이유는 표본의 크기가 커질수록, 표본정규분포에 가까워지기 때문이다.
- df 자유도에서 n-1을 하는 이유는, 표본으로 산출된 값은 항상 모수보다 작게 나오기 때문에, 보정해주는 개념이다.
- 평균이 0, 자유도가 증가함에 따라 분산은 1에 접근한다.

포아송분포 VS 지수분포 (헷갈림 주의)
- 포아송분포 : 일정한 시간이나 구간에서 발생하는 특정한 사건의 수를 변수값으로 하는 확률변수의 분포
- X : 건수 / 단위시간
- 지수분포 : 한 사건이 발생한 후에 다음 사건이 발생할 때까지의 시간이나 면적을 변수값으로 하는 확률변수의 분포
- X : 시간 / 건수, ex) 1건당 20분 (20분 / 1건)

포아송 VS 지수 (기대값)
- 포아송의 기대값은 (람다) 이지만, 지수의 기대값은 (1 / 람다) 이다.

지수분포 식 : (람다) * e^(-람다 * x), 평균 = 표준편차 = 1 / 람다
람다 : 일정한 단위시간이나 단위면적 등에서 발생하는 사건의 평균발생 횟수

[분산 관련 확률분포]


F-분포의 모양은 분자의 자유도(df)와 분모의 자유도(df)에 따라 달라진다.
F-분포 특징
- 확률변수 F는 항상 양의 값만을 갖는 연속확률변수이다.
- 카이제곱분포와 다르게 2개의 자유도를 갖는다. (집단이 2개니까)
- 2개의 자유도에 따라 분포의 모양이 변한다.
[시험 전, 한번 확인해보자]

'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (12) (0) | 2024.06.17 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (11) (0) | 2024.06.17 |
| 머신 러닝을 위한 통계학 필기 (9) (1) | 2024.06.17 |
| 머신 러닝을 위한 통계학 필기 (8) (0) | 2024.06.16 |
| 머신 러닝을 위한 통계학 필기 (7) (0) | 2024.04.18 |