[여기서부터 매우 중요, 기말고사 직접연계 부분]
[Chap. 7 : 확률변수 & 확률분포]
[기말고사 시험 : 6장 ~ 8장, 유인물, 확률분포, 확률변수, 확률밀도함수, 각 분포들, 기댓값 및 분산, 표준편차 부분 확인]

도수분포표는 계급(구간)에 있는 실제 수(개수)를 의미하며, 상대도수분포표는 비율의 개념이 들어간 것이다.

변수 VS 확률변수 (확률변수 정의 : 시험출제 가능성)
- 변수는 변하는 수정도의 개념이다. 하지만 확률변수는 아니다.
- 확률변수는 변하긴 하나, 예측이 불가능한 변수이다. 뽑을 때마다, 규모가 바뀌어 변하긴 하는데 예측이 되지 않는 것이다.
- 추가로, 상수는 항상 같은 수를 말한다.
P(A ∩ B) ≠ P(A) * P(B) → 독립이 아니다 라는 의미를 담고 있다.
※ 뒤에서 다루겠지만, 주변확률 (한계확률)의 개념을 잘 알고 넘어가자.

[ 주변확률 * 조건부확률 = 결합확률 ]

확률 : 경험 혹은 실험결과로 특정한 사건이 발생할 가능성
변수 : 관찰대상의 속성을 척도로 측정하여 그 결과를 수치로 기록한 값들을 대표하는 말이다.

확률변수
- 확률변수란, 표본공간상의 모든 표본점들에 수치를 부여하는 규칙이다.
- 집합의 개념으로 생각하면 좋을 것 같다.
- 표본공간(집합공간) → 실수공간
- 이때 확률변수의 개념이 쓰인다.
- 모집단에서 추출된 표본의 특성을 나타내는 통계량은 확률변수이다.
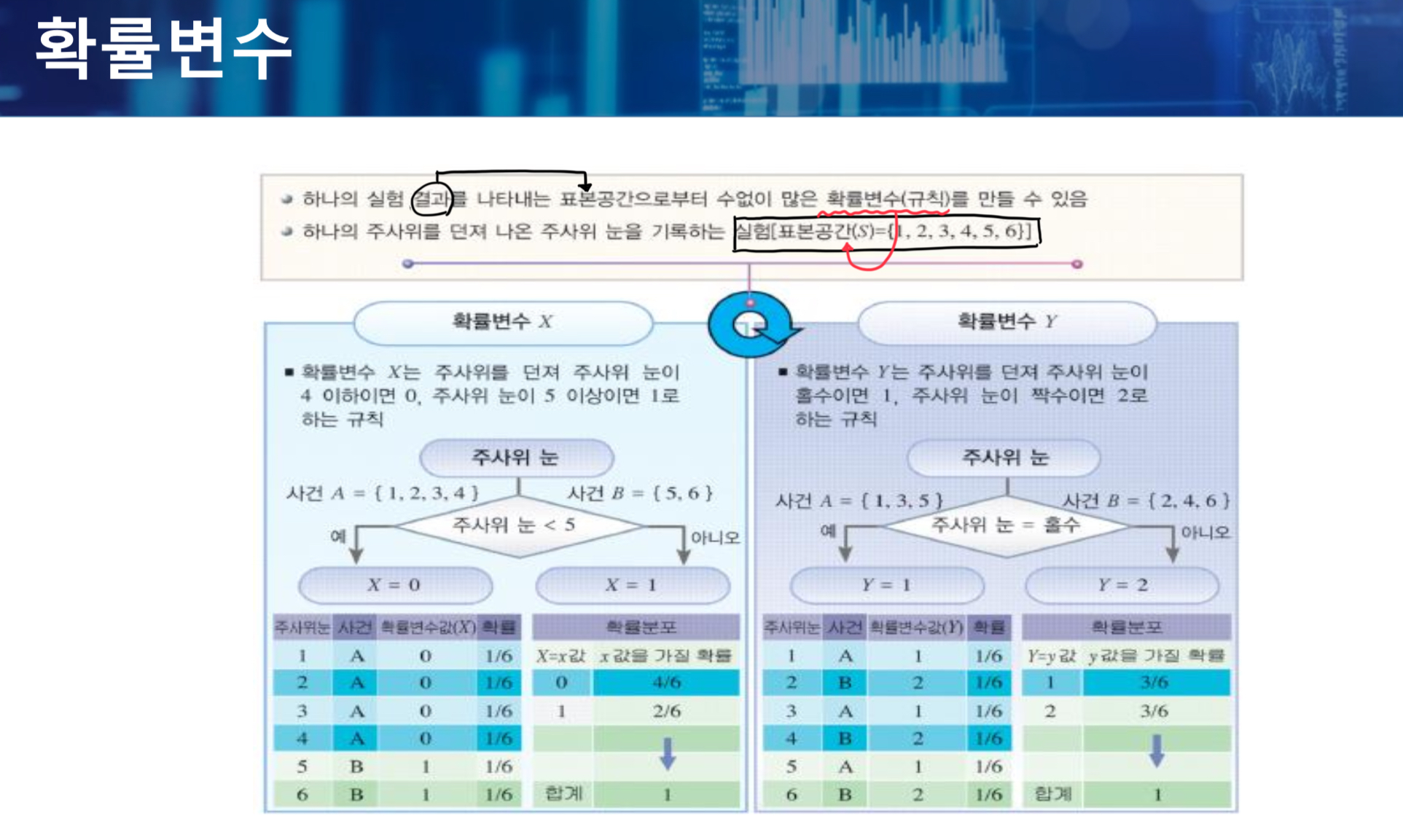
하나의 실험 결과를 나타내는 표본공간으로부터, 수없이 많은 확률변수(규칙)을 만들 수 있다.
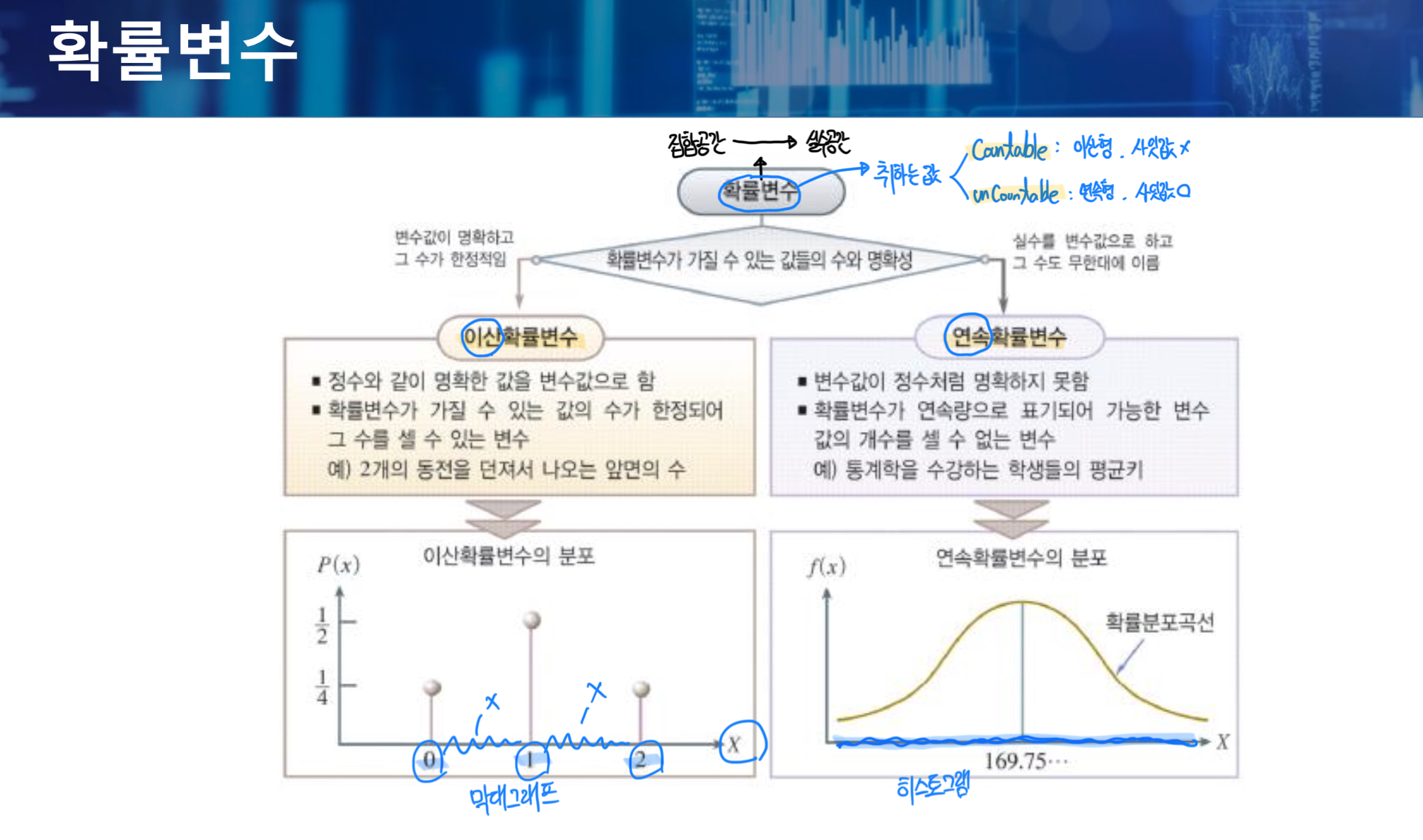
확률변수는 취하는 값이 이산형과 연속형이다.
- 이산확률변수는 정수와 같이 명확한 값을 변수값으로 한다. 사잇값이 존재하지 않는다.
- 연속확률변수는 변수값이 정수처럼 명확하지 못하다. 사잇값이 존재한다.
- 이산확률변수의 분포는 막대그래프, 연속확률변수의 분포는 히스토그램이다.
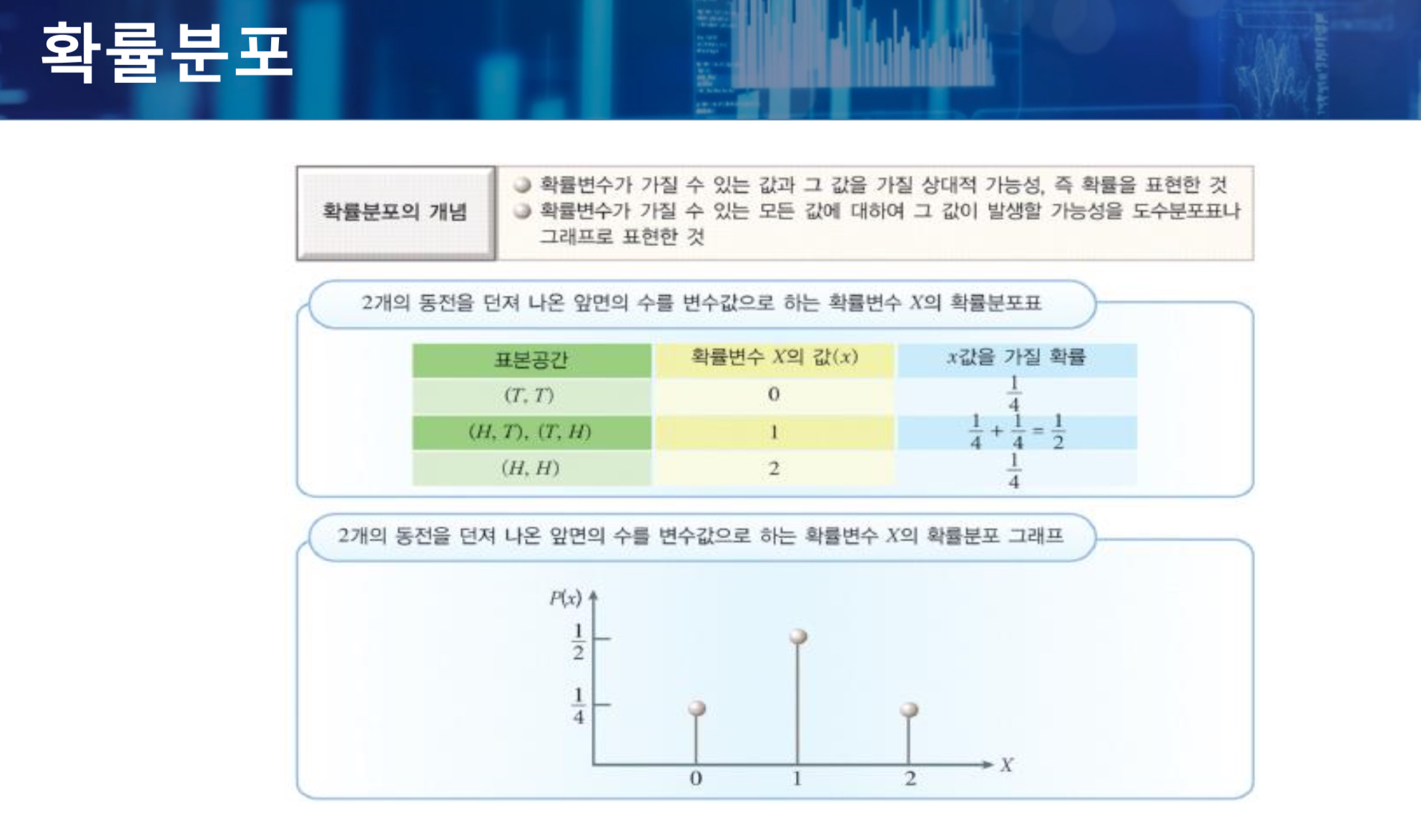
확률분포 : 확률변수가 가질 수 있는 모든 값에 대하여 그 값이 발생할 가능성을 도수분포표나 그래프로 표현한 것이다.

[이산확률분포]
이항분포
- 선택지가 2개이다.
- p 확률이 일정하다.
- 복원추출이다.
- 베르누이 시행을 무한번 시행한 것이다. (베르누이 시행은 딱 한번 시행하는 것이다.)
- X = 0, 1, 2, ..., n
초기하분포
- p 확률이 일정하지 않다.
- 비복원추출이다.
포아송분포
- X = 0, 1, 2, 3, ..., 무한 ∞
- 이산형인 이유?
- 화요일 아침 09:00 ~ 10:00시에 학교 정문에 통과하는 사람의 수
[연속확률분포]
카이제곱분포
- 연속형
- 집단이 1개
- 분산에 대한 분포
F분포
- 연속형
- 집단이 2개 이상일때
- 분산에 대한 분포
t분포
- 연속형
- 표본을 대상으로 한다.
- 개수가 적을 때 (변수의 개수가 30개 미만)
- 평균(중심)을 사용
정규 Z분포
- 연속형
- 모집단을 대상으로 한다.
- 개수가 많을 때 (변수의 개수가 30개 이상)

현재 시점까지의 특징을 가지고 해석하여 모델(분포)을 만들어 예측을 한 다음, 의사결정을 한다.
확률질량함수
- 확률변수 X가 이산확률변수일 경우, 확률분포함수를 P(X)로 표시한다.
확률밀도함수
- 확률변수 X가 연속확률변수일 경우, 확률분포함수를 F(X)로 표시한다.

연속형 ~ 확률밀도함수의 특징
- 전체 확률밀도함수의 면적 = 전구간에서 적분한 값 = 1
- 확률 = 적분한 값 = 면적
[이산확률분포]
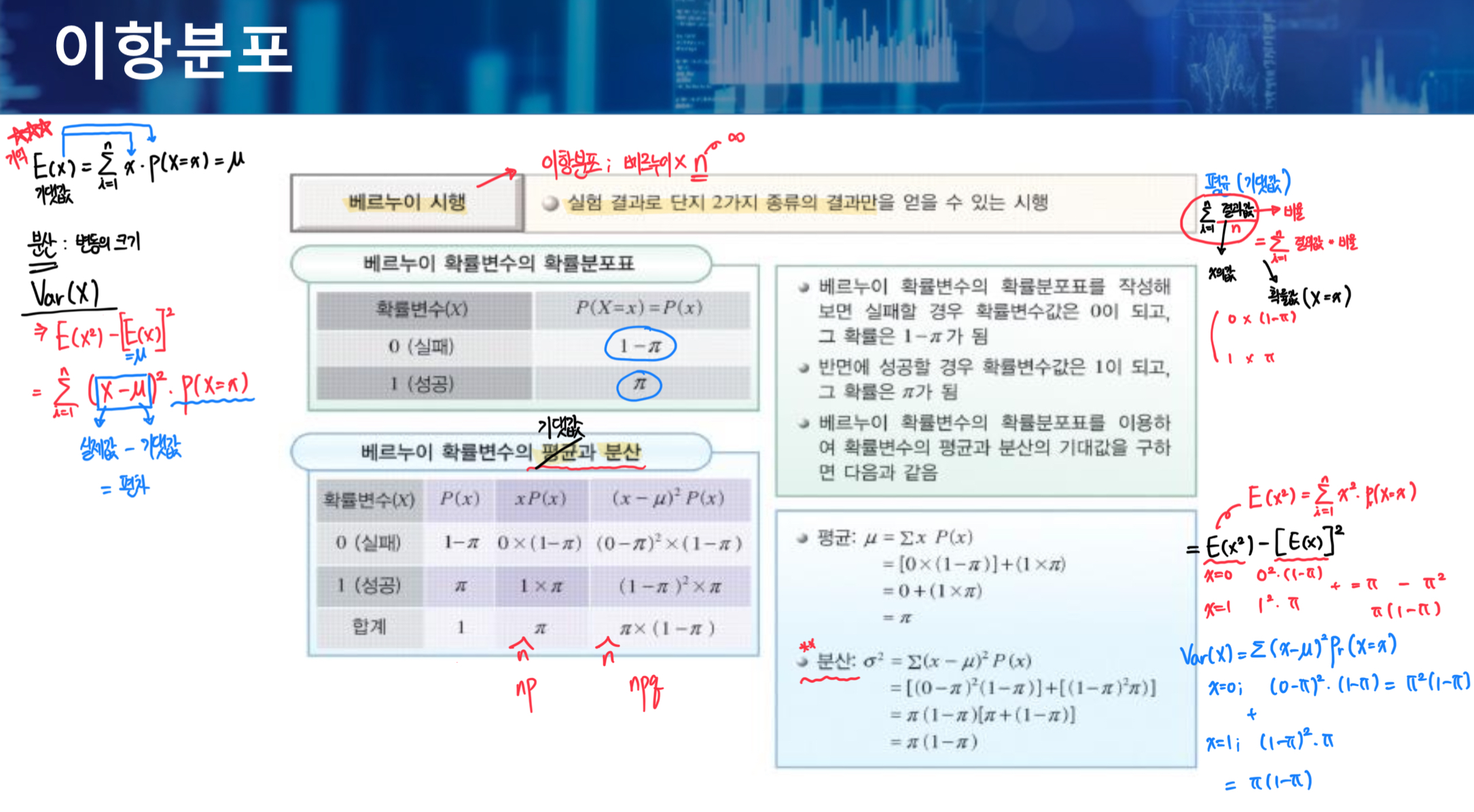
이항분포
- 이항분포는 베르누이 시행을 무한번 반복한 것이다.
- 베르누이 시행 : 실험 결과로 단지 2가지 종류의 결과만을 얻을 수 있는 시행이다.
- [ 시험 출제 ]
- E(X) = ∑ x * p(x) = 기댓값 = 평균
- V(X) = E(X^2) - [ E(X) ]^2 = ∑ x^2 * p(x) = 분산
- 분산은 변동의 크기를 의미한다.

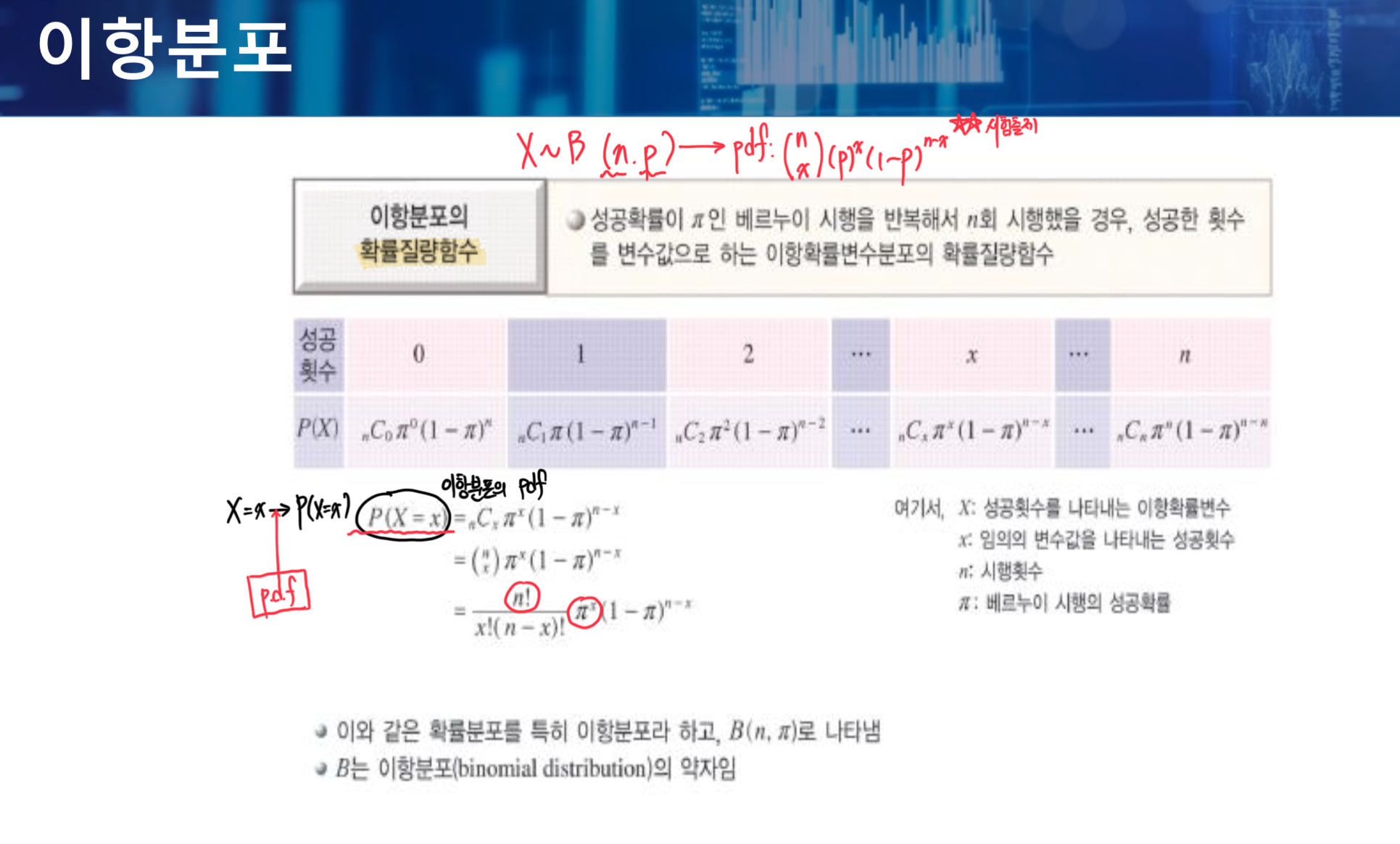
이항분포의 확률질량함수
- X ~ B(n, p) → p.d.f : (n번 중 x번 택) * (성공확률)^(x번) * (실패확률)^(n-x번)
- nCx * p^x * (1-p)^(n-x)
- 성공확률이 p인 베르누이 시행을 반복해서 n회 시행했을 경우, 성공한 횟수를 변수값으로 하는 이항확률변수분포의 확률질량함수

(초기하분포 식이랑 헷갈리지 말자.)
왜 이항분포?
- X : 흡연학생수 (이산형)
- 흡연/비흡연 여부이므로, 선택지가 2개이다.

- 기대값 = n * p = 시도횟수 * 성공확률
- 분산 = n * p * q = 시도횟수 * 성공확률 * 실패확률
- 확률변수, 개수 & 성공확률 → 이항분포
[시험출제]
- 확률변수의 필요성
- 확률분포의 정의, 종류, 각각의 특징
- 확률밀도함수 (P.D.F)
- E(X), V(X) 공식
'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (11) (0) | 2024.06.17 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (10) (1) | 2024.06.17 |
| 머신 러닝을 위한 통계학 필기 (8) (0) | 2024.06.16 |
| 머신 러닝을 위한 통계학 필기 (7) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (6) (0) | 2024.04.18 |