

결합확률 VS 조건부확률
- 결합확률 : 남학생이면서 사과를 좋아하는 학생일 확률
- 조건부확률 : 남학생 중에서 사과를 좋아하는 학생일 확률

독립 : 결과에 서로 영향을 주지 않는다!

사후확률을 구할 때에는 Decision Tree를 이용하자!!




베이즈 정리
- 베이즈 정리는 사전확률 (prior probability) 을 이용하여 사후확률 (posterior probability) 을 추정하는 데에 활용되는 정리이다.

[ 시험 출제 예상 문제 ]

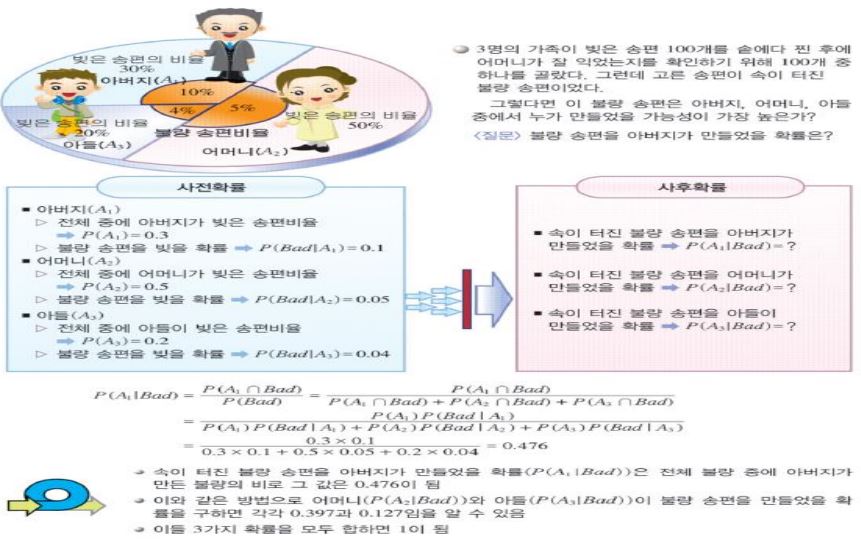
[ 필기 ]
분포 (Distribution) 특징을 정량화하는 데에 사용되는 값 : 중심, 산포
분포 : 집단의 특성을 나타내는 것
→ 집단의 특성을 정량화하는 데에 사용되는 값 : 중심과 산포
표나 그래프에서 중심은 무엇을 뜻하나 ?
▶ "목표" 에 대응한다.
통계의 시작은, 데이터가 측정을 통해 데이터가 생긴다. 즉 정량화하여 데이터가 생긴다.
정량화하는 데에 사용되는 것은 척도 이다. 척도는 도구이다.
기술통계량은 표본, 유한적인 모집단
근데 유한적인 모집단을 대상으로 기술통계량을 한다면, 추정통계량이 필요가 있겠나..? 그래서 대상은 표본으로!
분포의 형태 : Sample의 대표성 판단
- 왜도 (skewness) : 삐딱하냐?
- 첨도 (kurtosis) : 뾰족하냐 ?
예시)
산술평균 = 1/3(국어 + 수학 + 영어) = 1/3(국어) + 1/3(수학) + 1/3 (영어) = 값
1/3 이 가지고 있는 의미는 비율, 가중치, 중요도 이다.
즉, 모든 과목에 대한 중요도가 똑같다는 얘기이다.
편차 (deviation)
- 편차 : 평균을 기준으로, 실제값과 평균값의 차이
- 오차 (Error) : 참값과 실제값의 차이
- xi : i번째의 실제값
- u : 평균
모집단과 표본의 기호차이도 있다.
모집단의 크기는 N이라고 표현하며, 모집단에서 샘플링하여 나온 표본의 크기는 n으로 표현한다. (기호의 약속)
모집단의 평균편차에서의 절댓값을 씌운 이유
- 편차의 합은 0이기 때문에 0과 음수를 방지하기 위하여 절댓값을 씌웠다.
표본의 분산에서는 왜 n-1로 나누었을까? A. "정확도"
→ 표본분산을 n-1로 나누는 이유 (tistory.com)
표본분산을 n-1로 나누는 이유
통계에서 표본분산을 구할 때 n-1로 나누는데, 그 이유는 그냥 n-1로 나누는 것이 값의 정확도가 더 높기 때문이다. 단지 추측이기는 하지만 통계학이 발달하기 이전에는 표본분산도 n으로 나눴을
math100.tistory.com
첨도는 편차가 커질수록↑ 커진다.
왜도, 첨도 : 샘플링 데이터 문제
성별, 학점 : 질적자료 (척도), 성별 : 명목척도, 학점 : 서열척도
막대그래프 ≠ 히스토그램
데이터 (척도) VS 변수 (담는 그릇)
비율 VS 확률
- 동전 : 1/2 , 주사위 : 1/6 에서의 2와 6은 모든 경우의 수를 의미한다. 여기서 1/2과 1/6은 확률을 의미한다.
- 국어, 영어, 수학 평균을 낼 때의 1/3은 비율을 의미한다. 국어, 영어, 수학에서의 1/3은 확정적이지만 확률을 변동될 수 있기 때문에 윗개념과 아래개념에서의 수는 다르다.
피어슨의 왜도계수
- (3(평균값 - 중앙값)) / 표본의 표준편차 , (3(평균값 - 최빈값 / 표본의 표준편차)
확률밀도함수 ( PDF )
- 차이 : 집단의 특성이 각각 다 다르게 나온다.
- 그 이유 : view마다, 3차원에서 2차원으로 투영했을 때 (MAPPING) 모든 요소들이 반영되지 않기 때문이다.
- view1과 view2는 차원손실이 많이 일어난다.
- 해결 방안 : 모든 요소들이 반영될 수 있도록 하자.
- 투영했을 때의 범위를 분포, 산포라고 한다.
'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (7) (0) | 2024.04.18 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (6) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (4) (2) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (3) (0) | 2024.04.17 |
| 머신 러닝을 위한 통계학 필기 (2) (0) | 2024.04.17 |