다시 한번, 복습하자.
데이터란 무엇인가? 대상이 되는 집단을 구성하는 객체 (개체)들의 특징을 나타내는 변수들의 측정값 (FACT) 이다.
- 자료 : 사람, 물건, 조건, 상황을 묘사하는 것으로 기본적인 사실들의 집합
- 정보 : 의사결정에 도움이 되도록 가공되거나 요약된 형태의 자료
- → 데이터
확률 (Probability) VS 통계 (Statistics)
- 확률 : 하나의 사건, 개별적인 x
- 통계 : 집단의 사건, 여러 x들의 합
통계의 예시를 보자. 동전 던지기를 10회 시행했을 때, 개별 동전이 앞면이 나올 확률 1/2과 뒷면이 나올 확률 1/2을 신경을 쓰는가? 아니다. 앞면이 몇번 나왔고, 뒷면이 몇번 나왔는지를 신경쓴다.
조사에는 두 가지가 있다.
- 전수 조사 : 모집단 구성원 전체를 조사 및 분석하여 정보를 추출한다.
- 표본 조사 : (전수 조사에서 모집단을 통해 표본을 추출하고) 모집단을 대표할 수 있는 일부 대상을 표본으로 선정하여 분석한 결과로 얻은 정보를 이용하여 모집단에 관한 정보를 추정하고 검정한다.

※ 조사를 위하여 추출된 표본은 모집단으로부터 추출가능한 수없이 많은 표본 중의 하나에 불과하다!
예시로 사전조사 정확도 보다 출구조사 정확도가 높다.
그 이유는, 방금 투표를 끝낸 사람들을 대상으로 조사하기 때문이다.
표본추출과정
- 모집단의 확정 : 조사대상이 사람인 경우, 지역 및 시간 개념을 고려하고 인구통계학적 특성을 고려하여 모집단 결정
- 표본프레임의 결정 : 구체적인 실제 표본추출의 대상이 되는 표본프레임을 선정
- 표본추출방법의 결정 : 확률표본추출방법 VS 비확률표본추출방법
- 표본크기의 결정 : 신뢰구간접근법 OR 가설검정접근법을 활용하여 결정
- 표본추출



Q. 선호운동 도수빈도 그래프에서 조깅과 인라인 스케이트, 수영, 축구의 학생들의 응답수를 다 더한 후, 나누기 ‘종목 수‘ 해서 나온 값은 왜 의미가 없는 값일까? (평균의 개념)
A. 선호운동 도수빈도 그래프는 빈도 수를 나타내고 있다. 빈도 수는 최빈값과 관련이 있는데, 최빈값은 연산 자체가 의미없는 명목척도의 경우이다. 대표값으로 주로 사용된다.
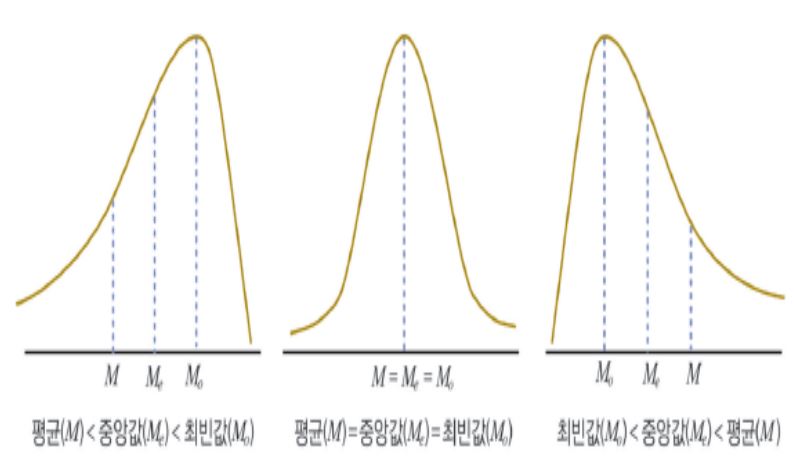
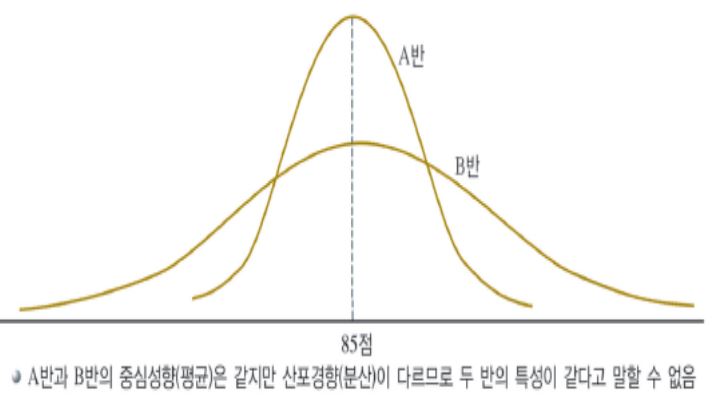
※ 이것 또한 매우 중요한 개념이다. 중심성향 즉, 평균이 같지만 분산 (산포경향) 이 다를 수 있다. 그래서 평균이 같다고 해서 두 반의 특성이 같다고 말할 수 없다!!

범위 : 변수값으로 측정된 값들 중에서 최대값과 최소값의 차이를 의미한다. ( MAX - MIN )

평균편차 : 절댓값으로 표시되는 편차들의 평균을 의미한다.

분산 : 편차제곱의 산술평균을 의미한다. 변수의 산포경향을 나타낸다.
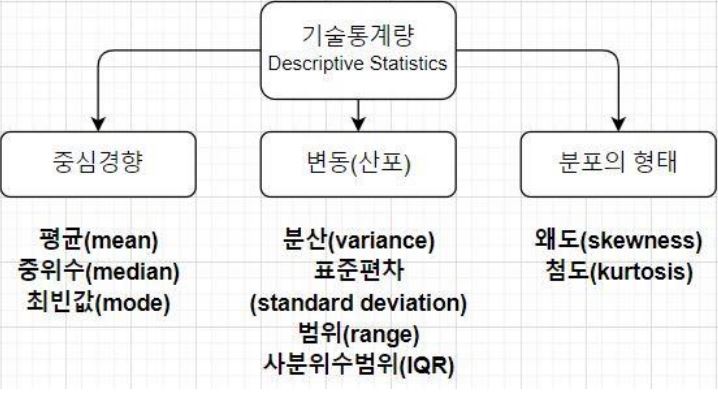
기술통계량 (Descriptive Statistics) : 분포의 형태 (왜도, 첨도)

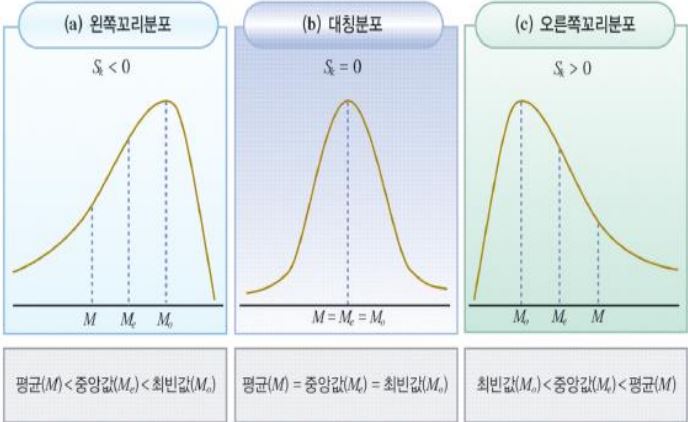
왜도
- 왜도는 분포의 비대칭 정도를 정량화한 값이다.
- 왜도 (비대칭도) 가 양의 값을 갖는 분포는 오른쪽에 꼬리가 길고, 음으로 치우친 분포는 왼쪽에 꼬리가 길다.
- 왜도(비대칭도)가 양 또는 음의 값을 갖는 분포 사례는 많이 있으며, 대표적인 사례가 소득 분포 데이터 세트에서 일반적이다.
- 소득분포 데이터 세트의 경우: 상대적으로 소득이 매우 높은 소수의 개인이 분포의 오른쪽 꼬리를 밀어주게 된다
- 왜도가 0이 아닌 즉, 비대칭의 분포를 하는 데이터를 통계 분석할 때에는, 특이치(outliers)의 영향과 특이치로 인한 잠재적 치우침(bias)를 고려하는 것이 중요하다.

첨도
- 첨도는 분포의 뾰족도 또는 평탄도를 정량화한 값이다.
- k > 0 : 정규 분포에 비해 첨도가 높고 꼬리가 두껍다.
- k < 0 : 봉우리가 평평하고 꼬리가 얇다.
- k > 0 : 극단적인 값이 상대적으로 더 자주 발생하는 경우를 의미한다.
- ▶ 일반적으로 극단적인 값이 더 많이 나타나는 분포로서, 이는 일부 데이터가 다른 데이터 보다 훨씬 더 크거나 , 작은 경우에 발생할 수 있다.
- 예) 주식 시장의 수익률 데이터 분포는 종종 꼬리가 두꺼운 분포를 보인다. 이는 주식 시장에서는 급격한 변동이 발생할 수 있으며, 일부 주식의 수익률이 극단적으로 높거나 낮을 수 있기 때문이다.
- 예) 지진 발생 강도 데이터 분포로도 종종 꼬리가 두꺼운 분포를 보이며, 이는 대부분의 지진이 상대적으로 약한 강도를 가지지만 일부 지진은 매우 강한 강도를 가질 수 있기 때문이다.
- 꼬리가 두꺼운 분포 (k > 0) 를 다룰 때는 이상치(outliers)가 더 많을 가능성이 있기 때문에, 이상치 처리가 매우 중요하다.
- 𝐾 ≠ 0 인 경우, 데이터 세트의 분포가 정규분포와 다른 수학적 특성을 가지므로 평균 및 분산과 같은 통계량 추정에 많은 영향을 미칠 수 있다.
- 예를 들어 데이터 집합이 정규분포보다 더 두꺼운 꼬리를 갖는 경우, 극단적인 값이 평균 계산에 포함되어 편향(bias)되거나 부정확한 결과를 초래할 수 있다.
- 마찬가지로 더 두꺼운 꼬리의 데이터로 인해 데이터의 변동성이 증가하여 분산 추정치가 커질 수 있다.

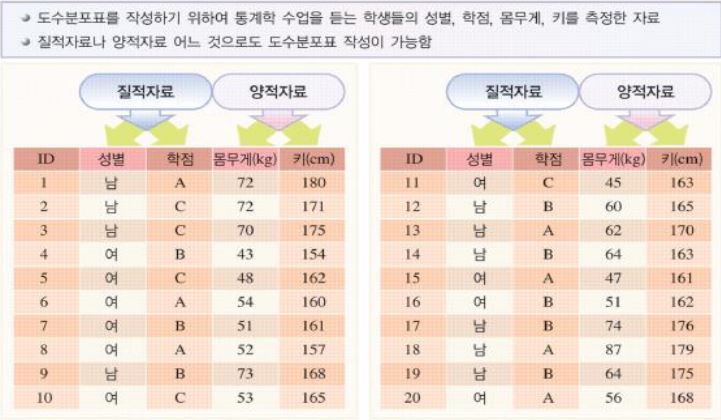
변수와 척도
- 질적 변수 : 명목척도, 서열척도 (질적척도)
- 양적 변수 : 등간척도, 비율척도 (양적척도)
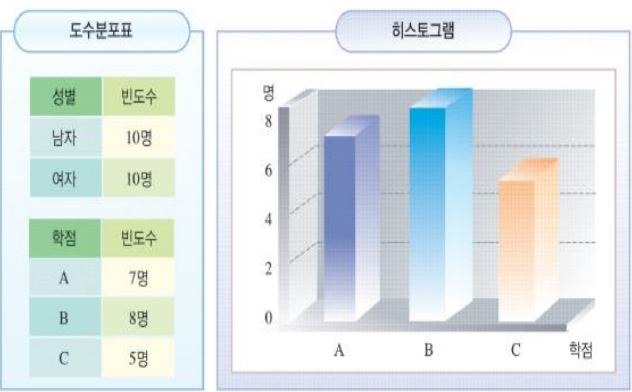

[ 필기 ]
Random 은 무질서가 아니다. 값을 모르는 것 뿐이지, 랜덤하게 값을 가지고 있다. 집단이 되면 분포를 지니고 있다.
- 확률 ↔ 개별 (each)
- 통계 ↔ 집단 (group, 분포를 지니고 있다.)
분포는 어떻게 알 수 있나?
- 집단이 지니고 있는 특성, 통계량을 (중심 → 평균, 산포 → 분산) 가지고 파악한다.
'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (6) (0) | 2024.04.18 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (5) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (4) (2) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (2) (0) | 2024.04.17 |
| 머신 러닝을 위한 통계학 필기 (1) (0) | 2024.03.04 |