[ 배경 지식 ]
모수 ↔ 통계량
확률적 관점 : 이미 알고 있는 모집단에서 어떤 사건이 일어날 확률에 관심이 있다.
※ 이미 알고 있는 모집단 이라면, 시점, 대상, 알고있는 특성을 말한다.
여기서 중심, 산포를 가지고 모수(특성)를 파악한다.
통계적 관점 : 표본에서 얻은 정보를 이용하여 미지의 모집단을 미루어 짐작하는 추론에 관심이 있다.
※ 데이터 (DATA)를 가지고 통계 (PROCESS) 를 거쳐 정보 (INFORMATION) 을 알아낸다.
통계를 적용할 때 한 가지 주의해야 할 점
- 통계는 목적에 따라 다르게 이용될 수 있다는 점이다.
- 이러한 통계적 해석의 오류를 범하지 않기 위해서는 상황을 고려하여 해석되어야 한다는 점이다.
★ 통계학에 사용되는 가정은 크게 두 가지 : 1) 데이터에 대한 가정, 2) 모델에 대한 가정
- 질 좋은 데이터란 자료의 대표성과 측정의 정확성이 결정짓는 중요한 두 가지 요인
- 자료의 구조가 모델의 적절성을 결정한다. 자료가 범주형? 연속형? 시계열 자료? 공간자료? 계층적 구조를 가진 것? 등의 정보들이 데이터 품질을 결정한다.
대표성 ?
- 어느 한 쪽으로 치우침이 없다. (치우침 X)
- 치우침 : 편의 (bias)
모델 ?
- 예시로 회귀모델 (Regression Model) 이 있다.
- → 선형수식 (Y = a + b * x + ...)
- 모델이 생성되었다는 말은, Process에 대한 결과가 도출될 수 있다는 말이다. 해석이 되었다는 얘기이다.
- 모델은 미래에 대한 예측이 가능해진다.
빈도론 VS 베이지안
통계적 머신러닝을 위해서는 확률의 두 가지 큰 축인 빈도론과 베이지안(Bayesianism)을 이해해야 한다.
※ 빈도론은 사전확률 (이론적) 을 말하고, 베이지안은 사후확률 (실증적 확률) 을 의미한다. 머신러닝에 있어서 "베이지안" 이 더 중요하다!! [ N번 시행 X : 결과 P = X / N ↔ 비율 ]
- "동전을 던졌을 때 앞면이 나올 확률이 50% 이다." 라는 진술에 대해,
- ▶ 빈도주의자 : "동전 하나 던지기를 수 천, 수 만번 하면 그 중에 50%는 앞면이 나오고, 50%는 뒷면이 나온다"라고 해석한다.
- ▶ 베이즈주의자: "동전 하나 던지기의 결과가 앞면이 나올 것이라는 확신은 50%이다"라고 해석한다.
- 빈도주의자는 확률을 객관적 확률로 해석하고, 베이즈주의자는 주관적 확률로 해석한다는 것이다.
빈도론자
- 빈도론에서는 여러 번의 실험, 관찰을 통해 나타난 사건의 빈도를 기반으로 모델(파라미터)에 대해 추정과 가설검정을 실행한다.
- 확률모델의 파라미터(θ)가 고정되어 있다는 관점에서 관측 결과의 변화를 분석한다.
“검진결과에 의해 암에 걸렸을 확률이 90%이다.” 라는 결과에 대한 해석
- 빈도주의(의사 관점) : 이러한 검진결과를 가진 환자는 정밀검사를 하면 100에 90명은 암에 걸려있다.
- 베이지안(환자 관점) : 자신이 암에 걸렸음을 주장하는 의사의 주장이 사실일 가능성(신뢰도)가 90%이다.
확률 VS 비율
- CASE 1 : 게임에 참여하는 비용은 4000원이다. 앞면이 나오면 10,000원을 따고, 뒷면이 나오면 2000원을 가져가는 것이다. 과연 이 게임에 참여하는 것은 이득일까? 기댓값을 알아보자. 50%확률로 앞면과 뒷면이 나오니, +6000 * 0.5 + -2000 * 0.5 = 기댓값은 +2000원이다. 0.5를 곱해준 값은 일어났을 때의 기댓값을 말한다. 그러므로 참여하는 것 이득이다. 이 때, 앞으로 일어날 것을 확률이라고 한다.
- CASE 2 : 3개의 과목 평균 점수를 알아볼 때, 예를 들어 1/3 * (80 + 90 + 100)에서 1/3은 과목 수만큼으로 고정되어 있다. 고정되어 있는 것을 비율이라고 한다.
빈도론의 문제점 ?
- 무한번 시행을 해야만 정확한 값을 알 수 있다는 것이다.
- 반복시행 자체를 할 수 없는 경우에도 빈도확률의 개념을 사용한다.
- 예를 들어 "다음 대선에 ○○○가 당선될 확률"을 생각해보자. "다음 대선"이라는 것은 역사상 딱 한 번만 일어나는 일인데다가 이 확률을 우리는 그 이전에 계산해내고 싶은 것이다. 하지만 우리는 이 경우에도 여러가지 관련된 사실을 이용하여 (여론조사 등을 이용해서) 이 확률을 생각해볼 수 있다.
- ★ 완벽히 조건이 같은 독립적인 반복 시행은 원칙적으로 존재하지 않는다.
예시를 들어, 동전 앞면 나오는 수를 10번 던졌을 때 나오는 수와 100번, 1000번 ... 던졌을 때 나오는 수는 분명 다를 것이다. 결국 1/2 (0.5) 에 수렴하겠지만, 무한번 하지 않는 이상 정확한 값을 알 수 없다. "추세가 중요하다."
확률의 개념
- 경험 혹은 실험 결과로 특정한 사건이나 결과가 발생할 가능성
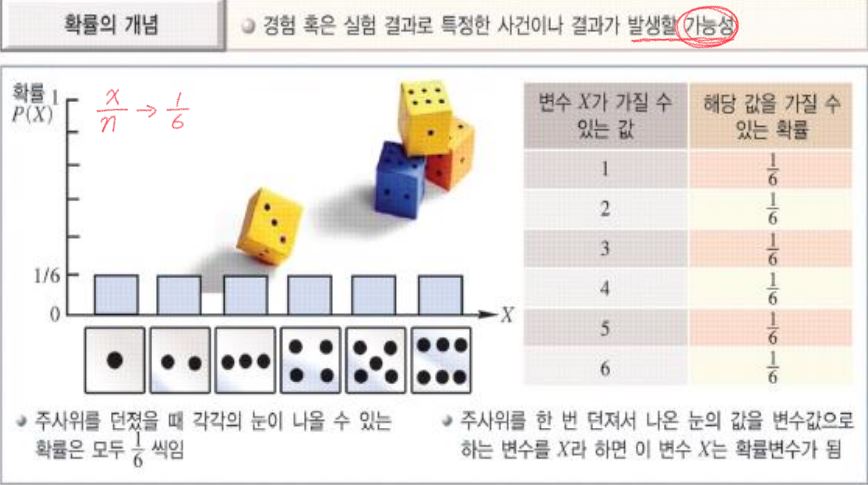

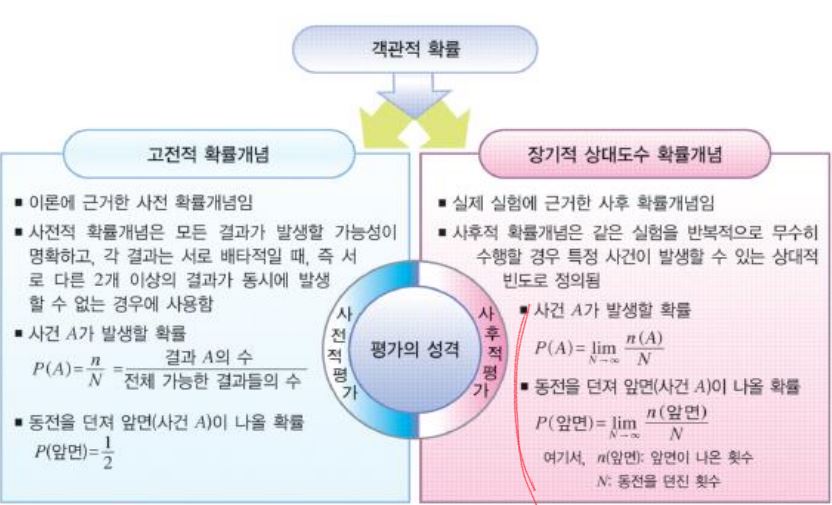
객관적 확률에는 두 가지가 있다. 고전적 확률개념과 장기적 상대도수 확률개념이 있는데 여기서 유심히 봐야할 것은 "장기적 상대도수 확률개념" 이다.
- 실제 실험에 근거한 사후 확률개념이다.
- 사후적 확률개념은 같은 실험을 반복적으로 무수히 수행할 경우 특정 사건이 발생할 수 있는 상대적 빈도로 정의된다.



★ 매우 중요 ★
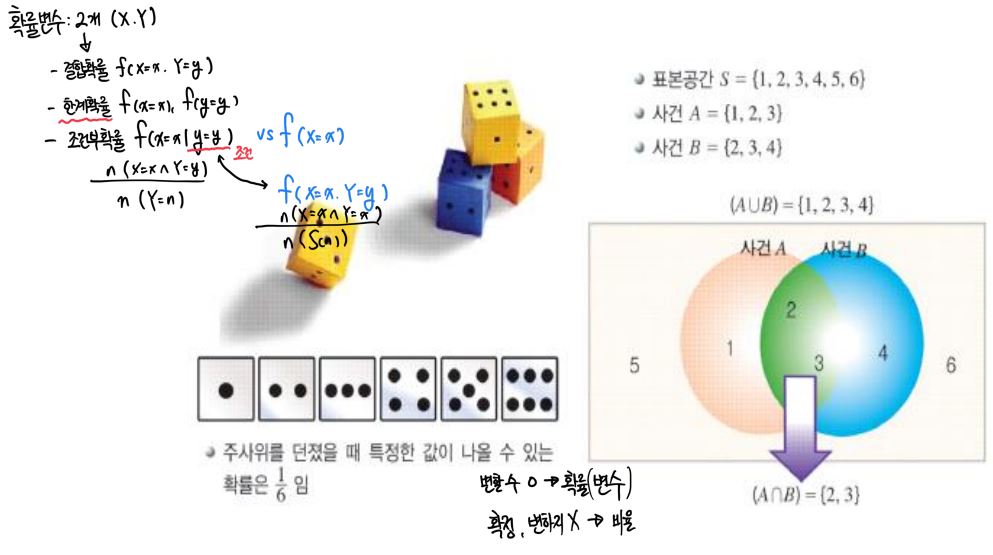
한계 확률 : 변수 두 개중에서 하나만 변수이다.
결합 확률 : 변수 두 개 모두 변수이다.

※ 확률 문제에서의 P(X = x) 를 자주 볼 수 있는데, 여기서 큰 X는 확률 변수를 의미하고, 작은 x는 X의 결과값을 의미한다.

- 여기서 '사과' 열에서 열의 확률 0.25는 P( X1 = 사과, X2 = . ) 를 의미한다.
- X2 = . 은 '모든 요소가 고려되었다' 를 의미한다.
- 여기서 '남자' 행에서 행의 확률 0.40은 P( X2 = 남자, X2 = . )
※ 결합확률이 헷갈려서 찾아보기 ...
https://datalabbit.tistory.com/17
[기초통계학] 확률(Probability) 2 - 결합확률, 주변확률, 조건부확률
Review 참고 포스팅 : 2020/05/20 - [Statistics/Basic Statistics] - [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 [기초통계학] 확률(Probability) 1 - 확률의 기본 개념 Review 참고 포스팅 : 2020/05/18 - [Statistics/Ba
datalabbit.tistory.com
여기서 참고를 하였다.
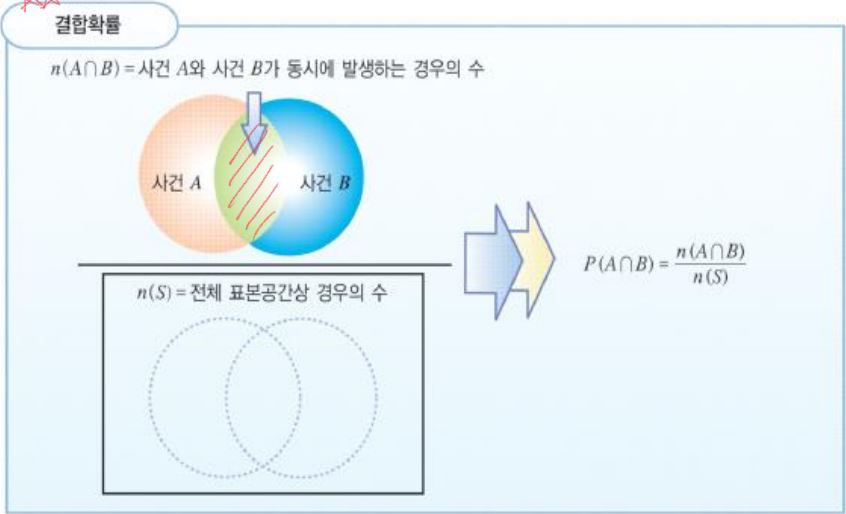
결합확률(Joint Probability)
- 결합확률이란 두 개의 사건이 동시에 일어날 확률을 의미한다.다르게 설명하면, 서로 배반되는 두 사건 A, B가 있을 때, 두 사건이 동시에 일어나는 확률을 P(A∩B) 라고 하며 이 확률을 A, B의 결합확률이라고 정의한다.
- 예를 들어 동전을 던지는 실험을 가정해보자. 이때 첫 번째 동전을 던지는 사건을 A, 두 번째 동전을 던지는 사건을 B라고 해보자. A, B는 동시에 일어날 수 없으므로 상호 배반이라고 할 수 있겠죠? A에서 나올 수 있는 경우의 수는 앞, 혹은 뒷면이며 B도 마찬가지이다. (H : 앞, T : 뒤)
| A (X) | B (Y) |
| H | H |
| H | T |
| T | H |
| T | T |
- 각각의 사건이 동시에 발생할 수 있는 경우의 수를 종합해봤다. 이때 H = 1, T = 0이라고 수치적으로 변환하고, 이에 따라 A와 B사건을 X, Y라는 확률변수로 변환해보자.
| A (X) | B (Y) | P(X, Y) |
| 1 | 1 | 1/4 |
| 1 | 0 | 1/4 |
| 0 | 1 | 1/4 |
| 0 | 0 | 1/4 |
위 각각의 사건이 나타날 확률은 서로 독립이므로, P(A∩B)=P(A) · P(B)를 만족한다. 따라서 각각의 결합확률을 우측 열과 같이 1/4이라고 할 수 있다.

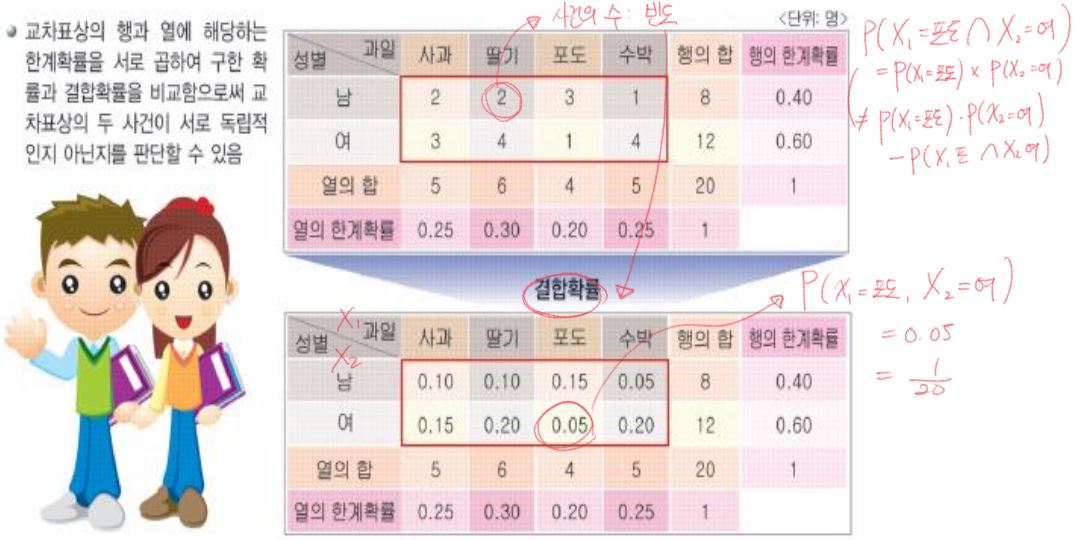
- 교차표상의 행과 열에 해당하는 한계확률을 서로 곱하여 구한 확률과 결합확률을 비교함으로써 교차표상의 두 사건이 서로 독립적인지 아닌지를 판단할 수 있다!

※ 조건부 확률 핵심
▶ 모집단의 크기가 다르다!!

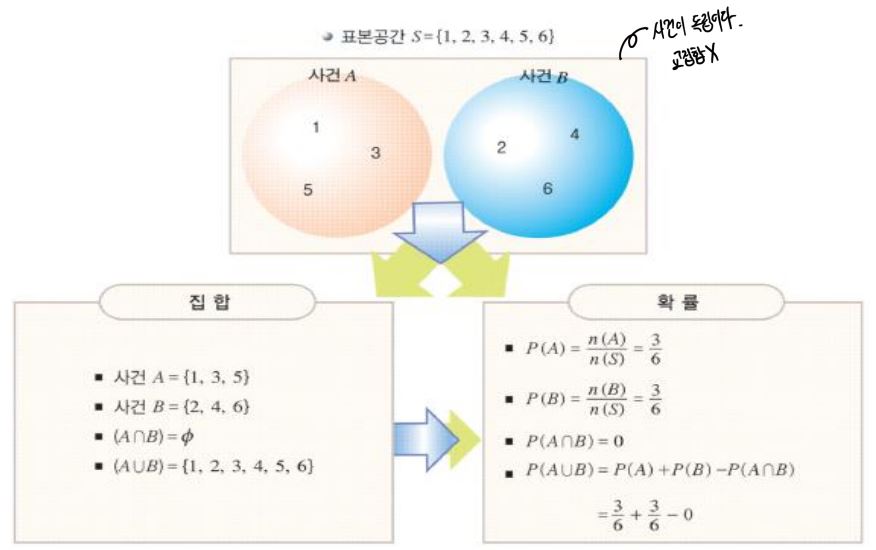
사건이 독립일 때? 교집합이 존재하지 않는다!!
독립 VS 배반
참고 : https://blog.naver.com/parkhc1992/220587985603
[확률과 통계] 독립사건과 배반사건
올해로 수능 수학강의 4년차. 수능강의를 오랜기간 하다보니, 아이들이 보통 어떤 부분을 어려워하고 혼동...
blog.naver.com
- 독립인 경우, P(A) * P(B) = P(A∩B), 사건 A가 사건 B에 영향을 주지 않는 상태를 말한다.
- 배반인 경우, A∩B가 공집합인 경우를 말한다. 서로 배반해서 아예 공통분모가 하나도 없는 상태를 말한다.
[ 필기 ]
예시) m = 100, A = 40%, B = 38% 신뢰수준 = 95% → 의미성 부여 (신뢰성 ↑)
표준오차가 +- 1.5% (Case1 : A (39.5 ~ 41.5 %), B (36.5 ~ 39.5%)) 이랑 +-5%랑 있으면, 표준오차가 작은 것이 더 좋다.
막대 그래프(이산형 데이터) → 도수(빈도)분포표 → 확률분포표(연속형 데이터) → 확률밀도함수(PDF) ↔ 확률분포
막대 그래프 & 확률 분포표 → 히스토그램

- 이산확률 : 기호 P( )
- 연속확률 : 기호 F( )
'머신러닝을 위한 통계학1 > 수업 필기' 카테고리의 다른 글
| 머신 러닝을 위한 통계학 필기 (6) (0) | 2024.04.18 |
|---|---|
| 머신 러닝을 위한 통계학 필기 (5) (0) | 2024.04.18 |
| 머신 러닝을 위한 통계학 필기 (3) (0) | 2024.04.17 |
| 머신 러닝을 위한 통계학 필기 (2) (0) | 2024.04.17 |
| 머신 러닝을 위한 통계학 필기 (1) (0) | 2024.03.04 |