[기말고사 범위]
< Review >
회귀분석
- 단순선형회귀
- 다중선형회귀 (Y → 수치형)
- 로지스틱(logistic)회귀 (Y → 문자형, 이분형)


상관분석 (2개의 데이터, 독립과 종속으로 구분된 2개의 데이터 이상)
판별함수 (로지스틱의 이웃) → 양인지 음인지 구분
모수 (모집단의 평균, 분산, 등...) 을 모르니까, 추정과 검정을 한다!
- 추정 : 하나의 값을 추정
- 검정 (← 유의확률) : Output에 유의확률 (p-value) 이 나올 때, 검정
판별분석 (판별함수) : y = w0 + w1 * x1 + w2 * x2 + ... → 판별점수를 계산한다.
▶ 판별분석 : 데이터의 변수값 토대로 서로 구분되는 2개 이상의 집단에 대한 판별규칙을 도출하는 통계기법이다.
- 여기서 w1, w2, w3, ... 는 판별계수라고 한다.
- 판별점수를 계산해서 양호 (+), 보통 ( * ), 불량 (-) 으로 판단한다.
- 판별함수를 분류의 갯수가 적을 때 유용하다.
- 반면에, 분류함수는 분류의 갯수가 많을 때 좋다.
- y 는 3분형 (이상)의 문자 데이터를 예측한 값이며, 양호 또는 보통 또는 불량으로 판단되는 값이다.
로지스틱 VS 판별분석 차이 ?
- 로지스틱 : 2분형 (→ 지금은, 확장되어 3분형 이상도 가능하다.)
- 판별분석 : 3분형 (→ 지금은 2분형 또한 가능하다.)
- 하지만, 로지스틱과 차별화를 두기 위해 '정규분포'를 사용 + 등분산성
판별분석? 도대체 무엇인데?
- 과거의 기존 DATA를 가지고 모델링을 생성한다. 그런 다음 NEW DATA, Y를 예측한다.
- y = w0 + w1 * x1 + w2 * x2 + ... → 판별함수를 도출하여, 케이스별 판별점수를 계산한다. 계산이 끝났다면, 소속집단으로 분류한다.
- 예측모형의 핵심은, 새로운 데이터를 식(x, y)에 적용시켜서 추정, 검정, 분류표를 만들어 타당성을 만들다.
- 여기서 w1, w2, ... 는 판별계수이며, x1, x2, ... 는 예측변수이다.

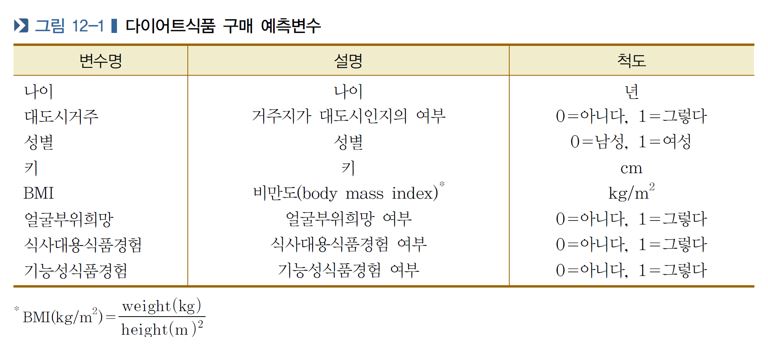
※ 판별분석 절차 [기말고사 시험 100%출제]
- 1) 예측변수 x1, x2, ... 선정 (전제조건 : 2분형의 명목척도)
- ex) 변수 : 다이어트 식품구매 여부 (1 : 구매, 0 : 비구매)
- 2) 판별함수 도출
- 3) 케이스별 판별점수 계산
- 4) 케이스별 판별점수에 따라 소속집단 분류 (예측)

판별분석을 위한 전제 조건
- 데이터의 각 개별 케이스가 어느 집단으로 분류되는지를 사전에 알고 있어야 한다.
- 종속변수는 집단을 구분하는 명목변수이어야 한다.
[기말고사 출제 100%]
판별분석 정의
- 판별분석(discriminant analysis)은 데이터의 변수값을 토대로 서로 구분되는 두 개 이상의 집단에 대한 판별규칙을 도출하는 통계기법이다.
-
집단이 두 개인 경우의 판별분석을 두 집단 판별분석(two-group discriminant analysis)이라 하고, 집단이 세 개 이상인 경우를 다중판별분석(multiple discriminant analysis)이라 한다.

※ 집단 간 차이분석


1. 가설 검정 (나이)
- H0 : 나이에서 구매, 비구매 비율이 같다.
- H1 : 나이에서 구매, 비구매 비율이 다르다.
2. 검정통계량
- F = 17.896 → p-value = 0.000
3. 기각역
- 1 - (0에서 17.896까지 f(F) dF 적분) = 0.000
- p-value = 0.000 < 유의수준 = 0.05
- H0를 기각한다.
4. 결론
- 나이에 있어서 구매와 비구매가 다르다.


※ 집단 중심값 (group centroid) : 집단별로 계산된 판별점수의 평균

※ 판별분석
- 판별함수 : 판별계수 → 판별점수 → 집단중심값
- 분류함수 : 분류집단의 갯수만큼 분류함수가 존재
- 1) 비구매 분류함수 → 분류 점수
- 2) 구매 분류함수 → 분류 점수
- → 분류 점수를 비교하여 큰 값으로 분류한다.
표준화 Z-Score (Z = (X - U) / 편차)
- 표준화 점수 : 상대적 위치 및 크기, 상대적 중요도 및 기여도를 알 수 있다.
분산분석 : 판별점수의 평균이 집단별로 유의한 차이가 있는지를 통계적으로 검정
- 1. 가설검정
- 1) H0 : 판별함수는 유의하지 않다.
- 2) H1 : 판별함수는 유의하다.
- 2. 검정 통계량
- F = 120.968 → p-value : 0.000
- 3. 기각역 (H0의 기각역)
- p-value = 0.000 < 유의수준 = 0.05 → H0를 기각한다.
- 4. 결론
- 980명의 표본 데이터에서는 판별함수의 판별점수가 구매와 비구매를 판별하는데 유의하다.

판별함수가 로지스틱과의 차이점 중에 등분산을 이용한다는 것이다. 그걸 이용하여 검정을 해도 된다.
- 1. 가설 검정
- 1) H0 : 모집단의 동일한 분산이다. (등분산이다.)
- 2) H1 : 모집단의 동일한 분산이 아니다.
- 2. 검정 통계량
- F = 9.371 → p-value = 0.000
- 3. 기각역 (H0의 기각역)
- p-value = 0.000 < 유의수준 = 0.05 → H0를 기각한다.
- 4. 결론
- → 모집단의 동일한 분산이 아니다라는 결론을 얻었다.




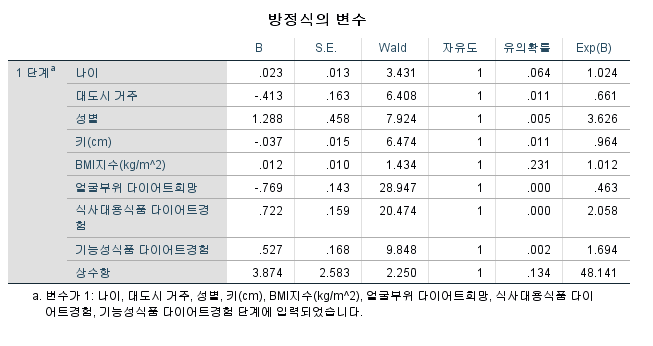


[판별함수의 도출]
- 계수를 예측하는 방법 → 최소자승법 (least square)
- 모형화에서 가장 쉽게 계수를 구할 수 있는 방법 → 계수들을 계산하여 나온 표 (12-6 그림)

모든 모형은 자기 서버의 데이터를 판별식에 넣어서 판별 점수를 구한 것
→ 예측값, 참값이 실제 결과와 판별점수에 따른 결과값을 구분하여 오분류 or 정확도 차이 구별한다.
집단 중심값 → 비구매한 사람들의 평균점수의 중심값 → 중요한 것은 집단중심값에 의해서 계산이 되어야 한다.
오분류율, 정확도율 → 오분류율이 작아야 정확도가 높다.
분류표 → 문자형 데이터일때는 항상 분류표가 나온다. → 얼마나 오분류율이 작으냐 ?
판별분석은 두 가지 방법이 있다.
- 1) 판별함수
집단중심값 / 1차로 판별계수를 계산 → 2차로 판별점수 계산 → 3차로 집단중심값을 계산 - 2) 분류함수
집단의 함수 개수 만큼 분류함수가 존재한다. - ex 비구매분류함수, 구매분류함수
- 분류점수 == 판별점수 (시험에서는, 분류점수라고 표기)
→ 분류점수로 비교하여 큰 값으로 분류한다. ex 658.310, 659.527 → 더 큰 것을 선택 - 양호, 보통, 분량 → 많아질 수록 복잡해진다. 그리하여 분류함수를 이용한다.

표준화
- Z score → 표준화점수 → 어떤 값의 상대적 위치 즉 상대적 중요도를 알 수 있다.
- 어떤 x란 값의 상대적 크기
- y에 미치는 상대적 중요도 (기여도)
- → 가장 높은 것이 식사대용식품경험
- 판별점수의 평균이 집단별로 유의한 차이가 있는지를 검정
착한데이터 : 이상치가 없는 것 → trim 한다 (이상치를 제거하는 것) → 모델의 정확도를 더 높이기 위해서
공분산행렬 → 동일한 분산이어야 한다 == 같은 크기의 분산들 (데이터들의 이상치가 없다는 의미)
'빅데이터 분석 > 수업 필기' 카테고리의 다른 글
| 빅데이터분석 필기 (10, 개념추가 + 실습) (0) | 2024.06.09 |
|---|---|
| 빅데이터분석 필기 (10) (1) | 2024.06.09 |
| 빅데이터분석 필기 (8) (0) | 2024.04.21 |
| 빅데이터분석 필기 (7) (0) | 2024.04.21 |
| 빅데이터분석 필기 (6) (0) | 2024.04.21 |