[군집분석]







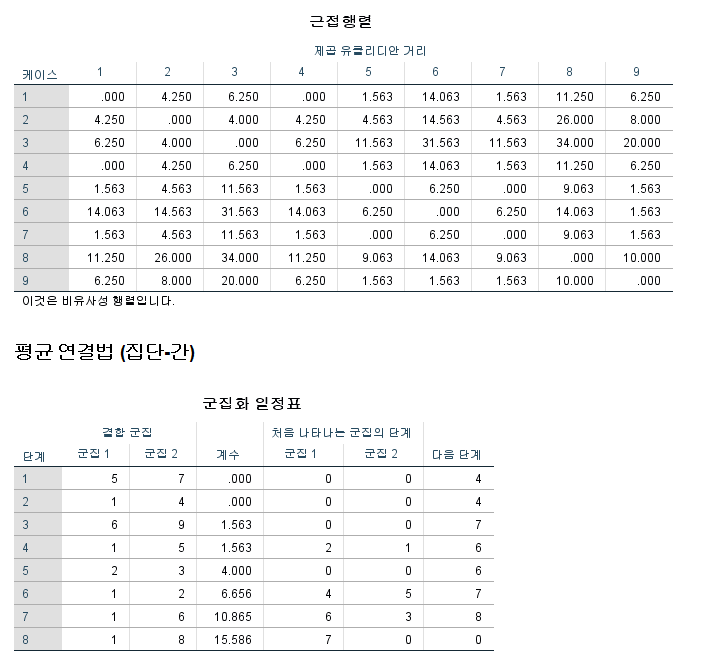



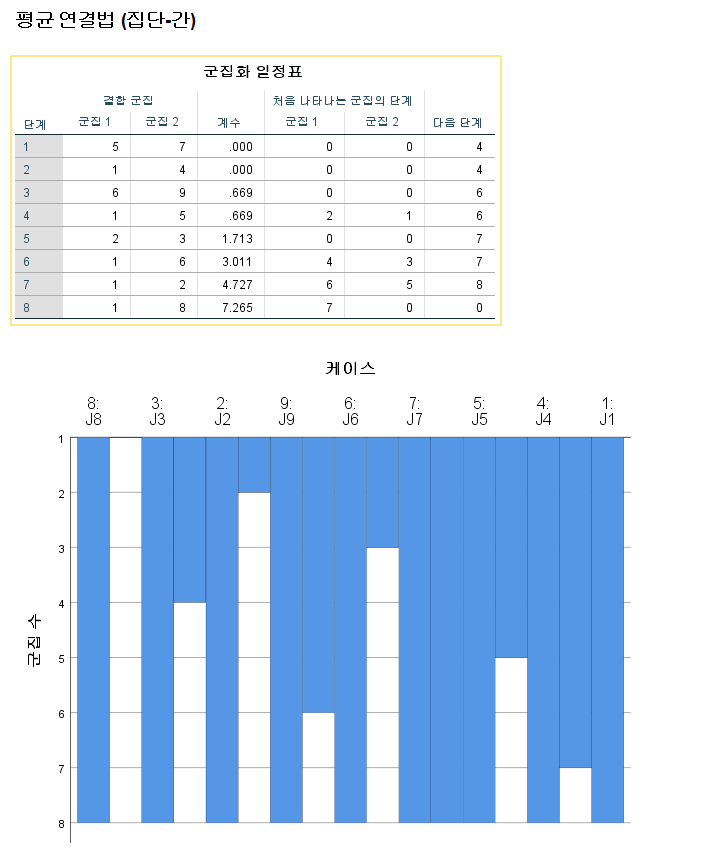

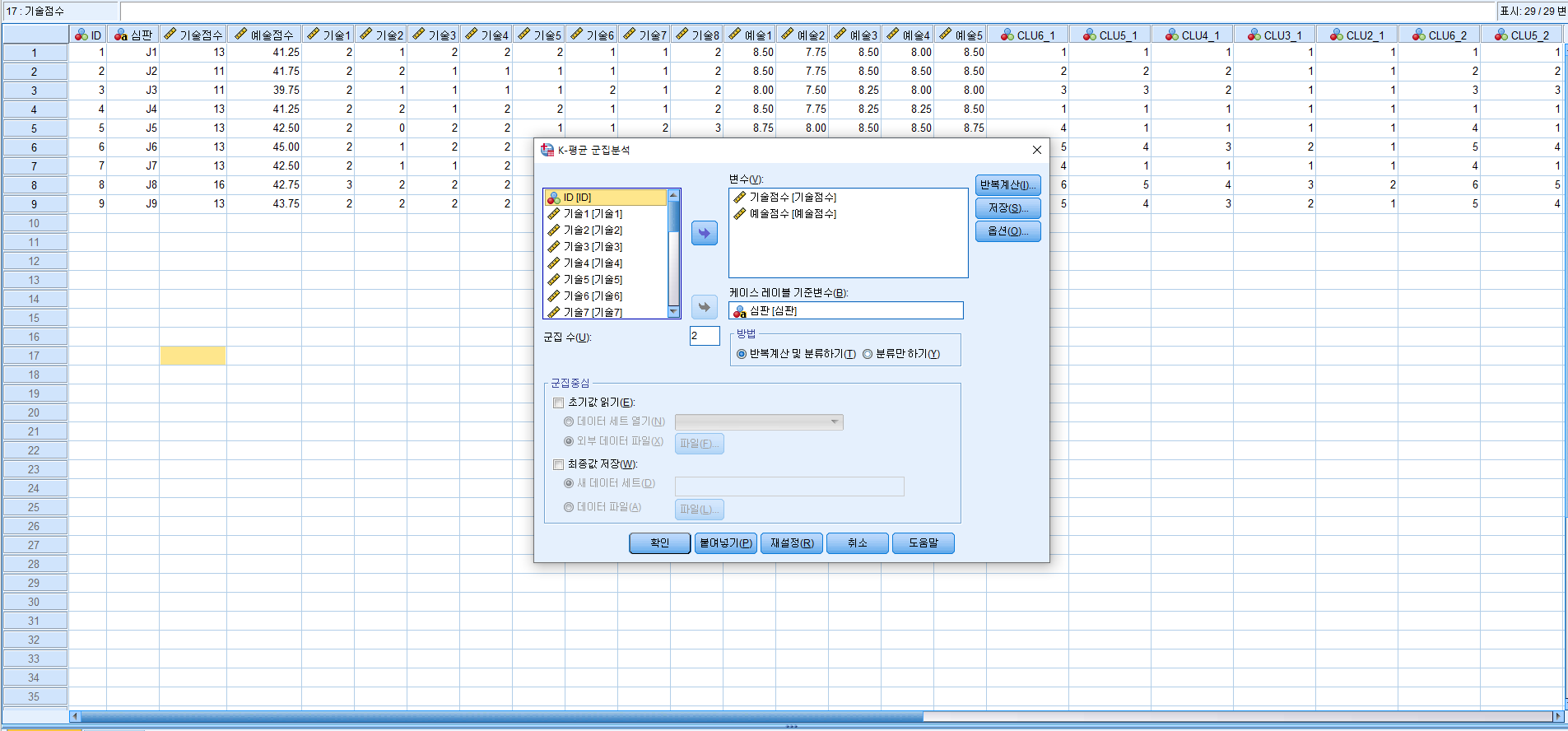


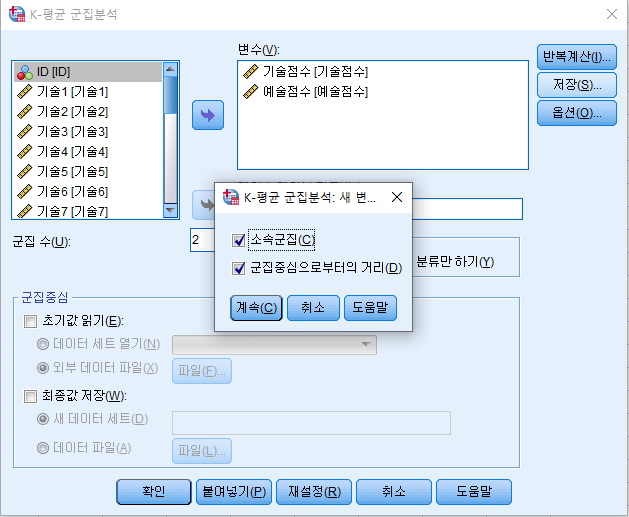


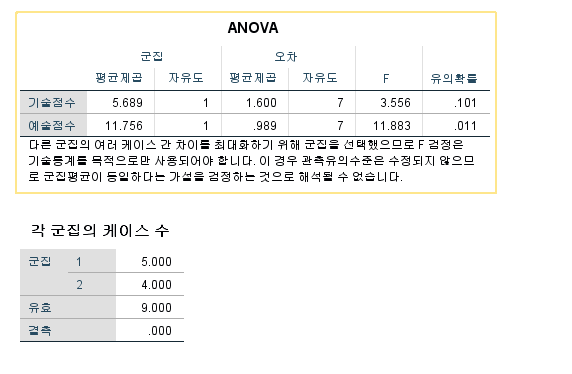
| ANOVA (분산분석) 표 | ||
| F - 검정 | 유의확률 (유의성 검정) | |
| 기술점수 | 3.556 | 0.101 |
이걸 봤을 때, 해석은 이렇게 할 수 있다. (시험출제)
1. 가설 검정 (모집단에 대해서!!)
- 심판 전체에 대한 ~
- H0 : 유의하지 않다. (== 군집을 나누는데 유의하지 않다.)
- H1 : 유의하다. (== 군집을 나누는데 유의하다.)
※ 유의하다는 것은 '의미가 있다'는 말과 동일하다.
2. 검정 통계량 : F - 검정 = 3.556
3. 기각역 : p -value = 0.101 > 유의수준 = 0.05 (Accept H0)
4. 결론 : 모든 심판의 기술점수는 군집분석하는 데 유의한 역할을 하지 않은 것으로 나타났다. OR 기여도가 없었다.
유의성 검정을 하는 이유는? 표본 계산을 통해 모집단을 알아보기 위해서
→ 전체에 대해서 유의성을 알아보는 것이 핵심이다.
검정(Test)은 전체 집합 (모집단) 미래에 대한 것
유의확률 : 검정 -> 검정의 대상은 (모집단, 전체, 미래)
전체를 알기위해 표본에서 유의확률을 구한 것이다.
표본에서 계산한 확률 = 유의확률
유의수준 : 모집단의 비교 기준
유의성 ~ 표본을 사용하니까 → 모집단
유의하다는 것 : 차이가 있다, 효과가 있다.
상관계수가 작다 = p-value값이 크다
상관계수가 크다 = p-value값이 작다 = 상관관계가 높다는 의미, 의미있다
[요인분석 실습] (뒤에서 배울 예정)
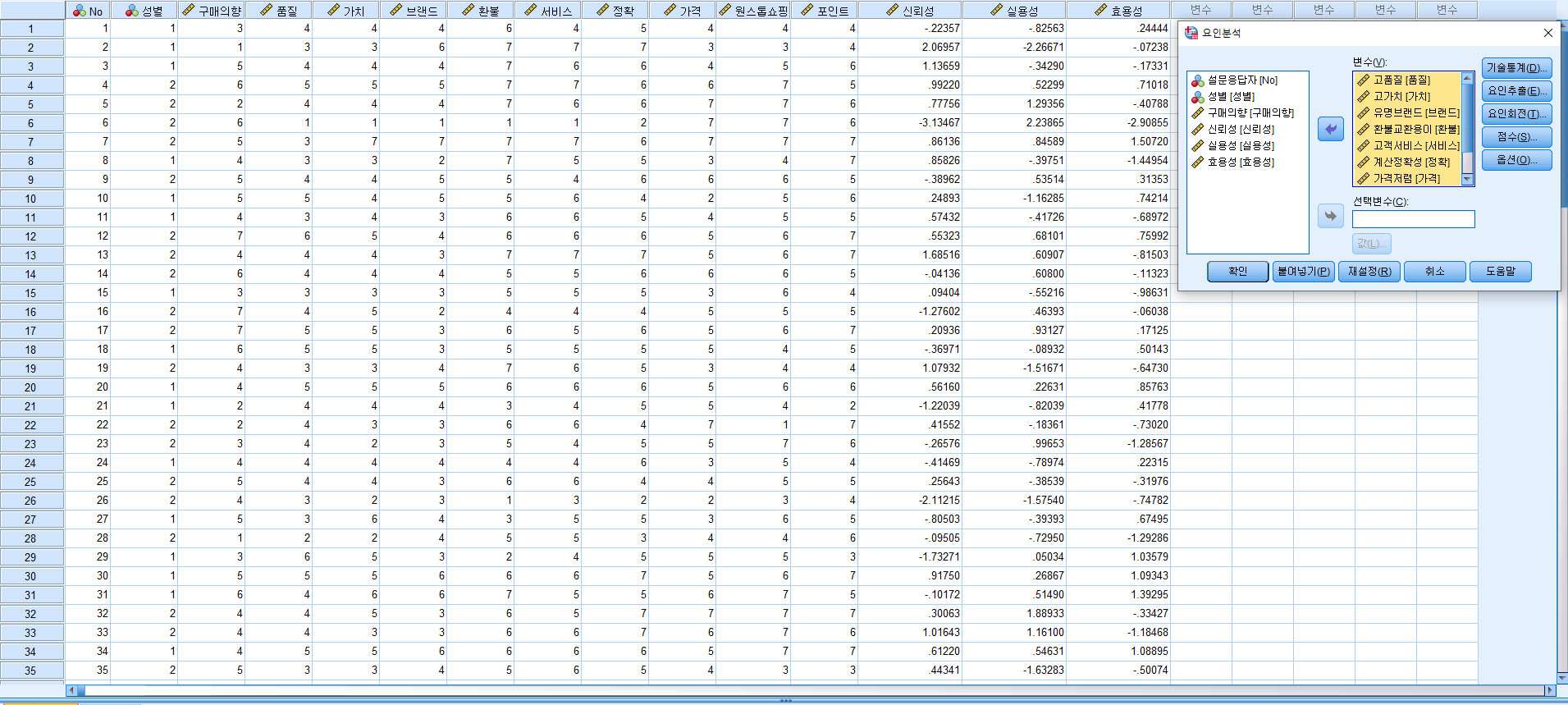


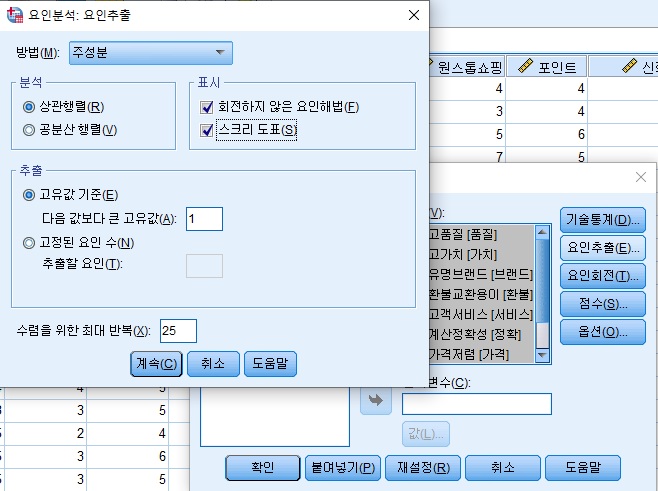

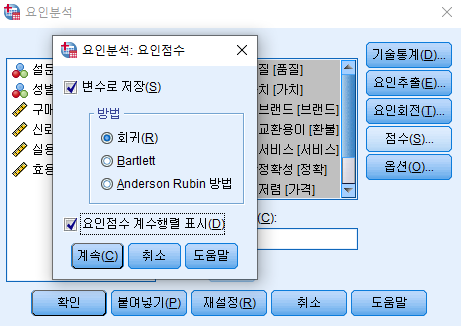
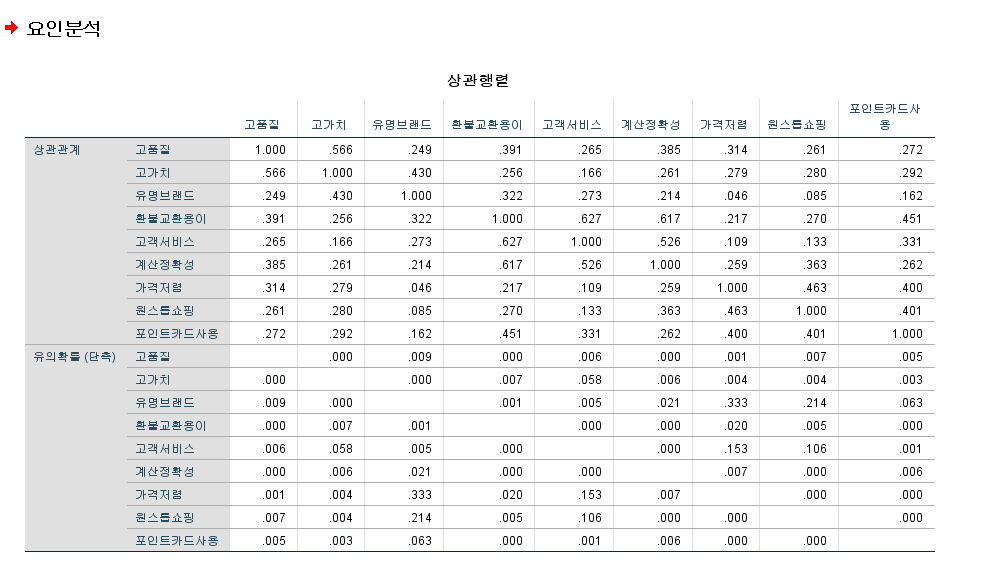

KMO
- 변수들의 상관성, 척도
- 상관관계를 나타내는 척도 OR 크기
- Barlett : 자신만의 논리로 검정
- 1) H0, H1 : 행렬상의 상관계수가 전반적으로 유의하느냐
- 2) 검정 통계량: 근사 카이제곱 = 245.45 → p-value : 0.000
- 바틀렛 공식을 사용해야 하는데, 사용하지 않고 카이제곱-분포함수를 이용한 것이 근사 카이제곱 (근사값)
- 3) 기각역 (H0의 기각역) : p-value : 0.000 < 유의수준 : 0.05 (Reject H0)
- 4) 결론 : 행렬상의 상관계수가 전반적으로 유의하다.
[ 공통성 ]
- 초기에는 1.000 값을 준 다음 추출된 값이 0.3 이하일 경우, 그 변수는 무시가 된다.
- 0.4 이상이여야, 공통성을 가진다.

[ 설명된 총분산 ] → 추출된 요인들에 의해 설명된 정도
- 성분이 9개일 때, 초기 고윳값 부분 전체 합은 9이다.
- 이 때 1보다 큰 값들만 추출하여 성분을 줄인다. 고윳값은 요인의 계수를 결정한다.


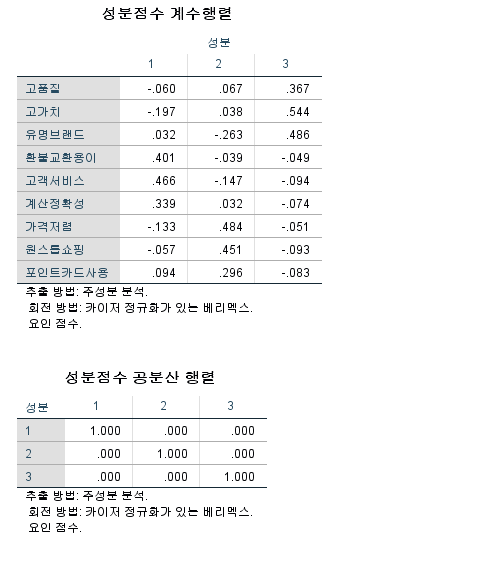
성분행렬 → 회전된 성분행렬
- 회전된 성분행렬이 핵심이다.
- 성분행렬의 계수는 상관계수이다. ex) 고품질과 성분1에 대한 상관계수
- 회전 : 각 성분이 어떤 변수에 속하는지 알아보기 위해 회전을 시킨다. (?)
- ex) Case1 : f1 = 고품질 * 0.216 + 고가치 * 0 + 0.265 * 품질 브랜드 + ...
- 구매의향을 y라 하고, 요인 9개를 요인 '신뢰성', '효용성', '실용성' 3개로 함축하여 계산한다.


'빅데이터 분석 > 수업 필기' 카테고리의 다른 글
| 빅데이터 분석 필기 (12) (0) | 2024.06.09 |
|---|---|
| 빅데이터분석 필기 (11) (0) | 2024.06.09 |
| 빅데이터분석 필기 (10) (1) | 2024.06.09 |
| 빅데이터분석 필기 (9) (1) | 2024.06.09 |
| 빅데이터분석 필기 (8) (0) | 2024.04.21 |