머신러닝2
- 지도학습 (기계학습의 회귀분석) -

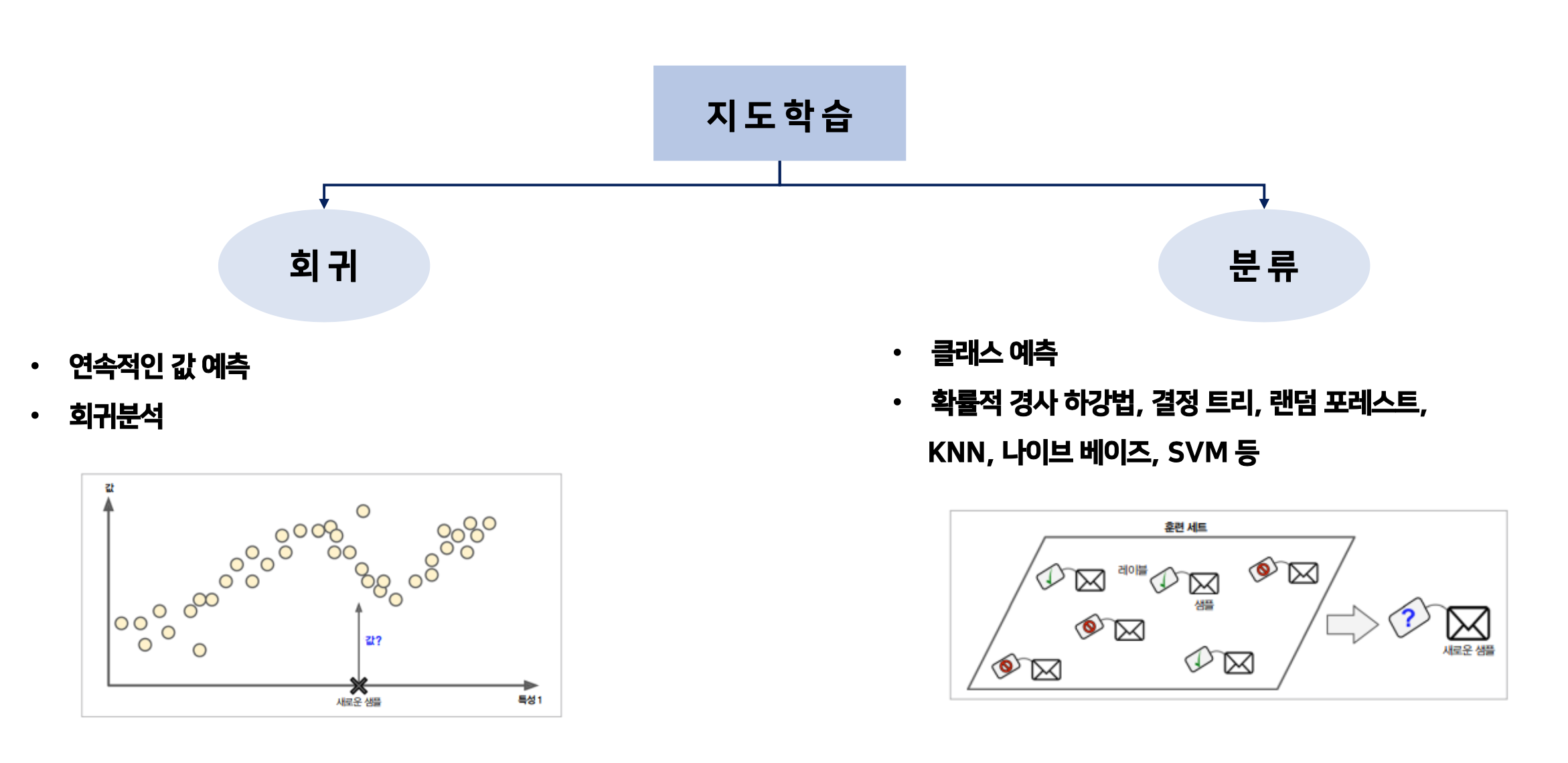
지도학습
- 다중 회귀분석 (Regression)
- 로지스틱 회귀분석 (Logistic Regression)
- 신경망
- 서포트 벡터 머신
- 의사결정나무
- 앙상블
- K-근접 이웃기법

회귀분석의 검정은 유의수준 (p-value) 로 한다. 기계학습의 검정은 예측의 정확도 이다.


최소제곱법은 회귀모형의 오차 제곱의 합 (SSE)을 최소로 하는 회귀계수를 이들의 추정치로 하는 것이다.

다수의 요소를 가지고 y를 예측하고 싶을 때, 이를 다중 선형 회귀분석이라고 한다.

다중 회귀분석
- 가설 (Hypothesis)에 대한 최적의 W와 b를 찾아 실제값과 예측값에 대한 오차 식을 비용함수 (Cost Function)이라고 한다.
- 회귀 문제의 경우에는, 주로 평균 제곱 오차(MSE)를 사용한다.

[매우 중요!!!]
경사하강법
- 회귀모형의 비용함수 MSE 최소화로 하는 반복적 접근 방식으로 회귀계수를 이들의 추정치로 하는 것이다.
- MSE와 SSE의 차이는 SSE는 데이터 값의 총합이지만, MSE는 데이터 값의 총합을 한 다음, 데이터 수만큼 나누어 준다.
- SSE : 데이터 셋의 모든 관측치에 대한 전체 오류를 제공한다.
- MSE : 관측치 수에 걸쳐 총 오류를 평균화한다.

비용 함수 (Cost Function) - 평균 제곱 오차 (MSE)
- 가설에서 세워진 식을 통해 예측값을 도출한다.
- MSE를 최소로 만드는 W와 b를 찾아서 회귀분석 식을 도출한다.
- 회귀 → 다양한 변수 → 표준화 (잔차)

Optimizer - backward
- Cost function을 최소화하는 매개 변수인 W와 b를 찾기 위한 작업을 할 때 사용되는 알고리즘을 Optimizer이라고 한다.
- 이를 머신러닝에서는 학습이라고 한다.
- 가장 기본적인 Optimizer 방법은 경사 하강법이다.
- Y = Wx + b에서 W의 크기가 지나치게 커지거나 작아질 때, 오차가 커지는 것을 알 수 있다.

- Cost가 가장 최소값을 가지게 하는 W를 찾아야 하는 것이 목적이므로, 볼록한 맨 아래 부분의 W값을 찾아야 한다.
- 접선의 기울기가 0 이 되는 지점이 Cost가 최소화 되는 지점이다.

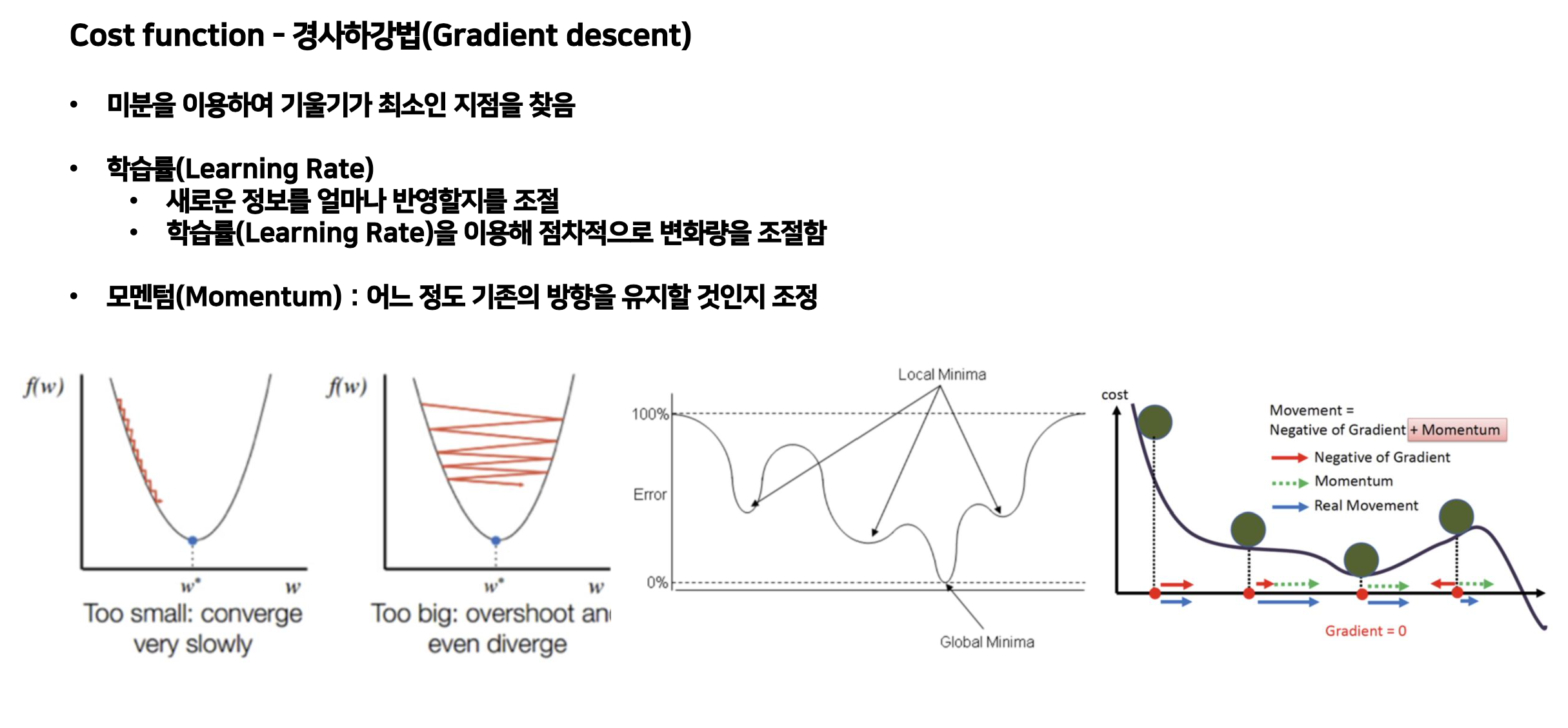
Optimizer - 학습률 (learning rate)
- W의 값을 변경할 때, 얼마나 크게 변경할지를 결정하는 값이다.
- 접점의 기울기가 0인 지점을 찾는 것에 있어, 어떤 크기의 폭으로 이동할지를 결정한다.

Optimizer - 학습률 (learning rate)
- 학습률을 적당하게 잡는 것이 매우 중요하다.
- 학습 횟수 (Epoch)를 통해 최적의 Low Cost를 찾는 것이 중요하다.

Optimizer - 최적의 Cost 결정의 문제
- 기계학습의 회귀분석 목적은 최적의 파라미터로 최소의 Cost (MSE)를 구하는 것이다.


Cost Function - 경사하강법의 프로세스 (Gradient Descent)
- 비용함수 : 예측 오류 또는 손실에 대한 정량적 측정을 제공하여 모델 성능을 수치적으로 평가
- → 최적의 매개변수를 찾는 것을 목표로 한다.
- STEP 1) 비용함수 정의
- STEP 2) 매개변수 편미분
- STEP 3) 매개변수 업데이트
- STEP 4) 반복한다.
- 데이터를 회귀 모델에 넣어 가중치를 업데이트하여 결과 값이 나오면 최소의 MSE를 구하기 위해 W값을 조정하며 반복한다.

'머신러닝2 > 수업 필기' 카테고리의 다른 글
| 머신러닝2 7주차 (2) - 코드 부분 (0) | 2024.10.23 |
|---|---|
| 머신러닝2 7주차 (1) (0) | 2024.10.23 |
| 머신러닝2 4주차(2) (0) | 2024.10.23 |
| 머신러닝2 4주차(1) (3주차는 추석일정으로 휴강) (0) | 2024.10.22 |
| 머신러닝2 2주차 (2) | 2024.10.22 |