
※ 제일 수업때 이해하기 어려웠던 부분이지 않을까 싶다... 정리를 하면서 우선 이해하는데에 초점을 맞출 예정이다...!!

▶ 서포트 벡터 머신은 우선, 분류를 위한 지도학습 방법이다. 그리고 이상치가 많거나 데이터의 결과 형태가 다양할 때 사용된다.
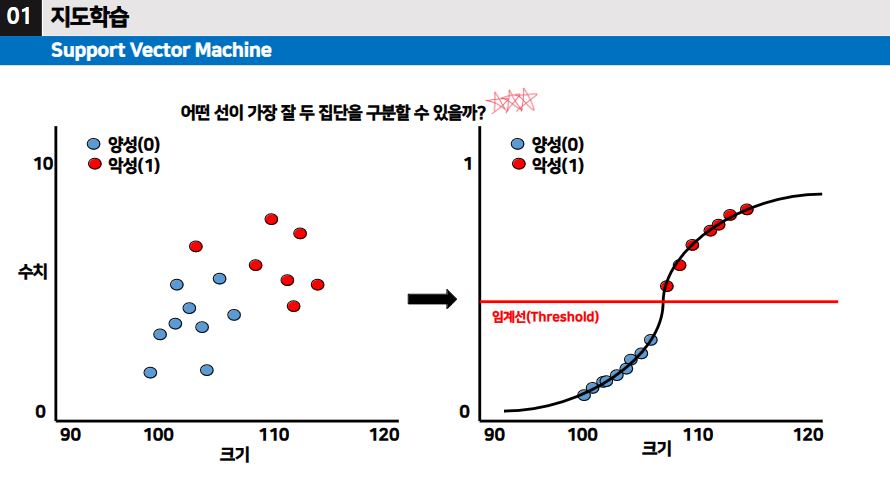

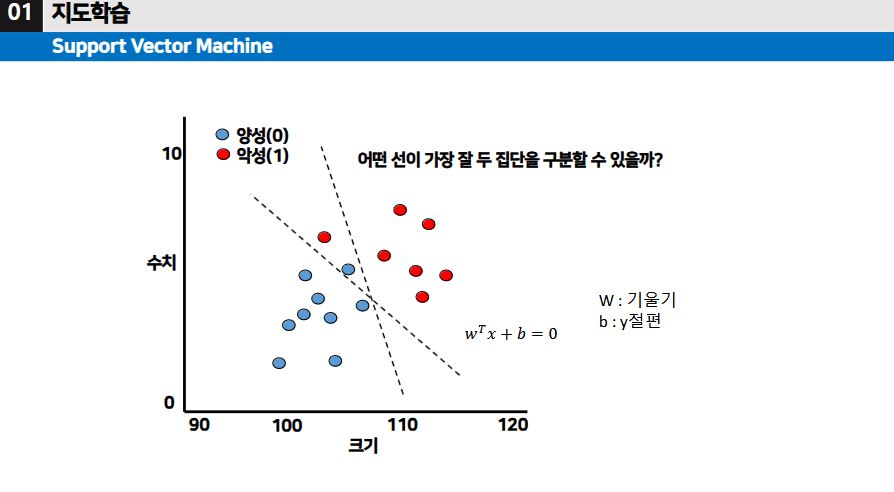
▶ 데이터가 다양하게 흩어져 있고 그 데이터들을 두 집단으로 가장 잘 구분하도록 선을 그어보는 것이 목적이다.

서포트 벡터 머신 (SVM)
- 퍼셉트론의 확장된 개념이다. 퍼셉트론 학습은 분류오차의 최소화이다.
- 하지만, 서포트 벡터 머신의 학습은 마진의 최대화이다.
- 장점으로는, 과적합되는 경우가 적고 고차원 분류 문제에 좋은 성능을 보이며 구조적이여서 매번 수행하여도 결과가 어느정도 비슷하다는 것이다.
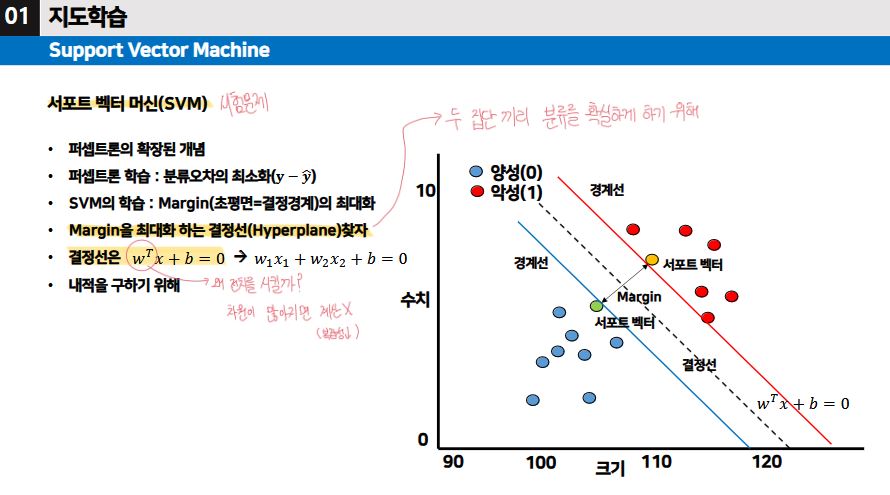

서포트 벡터 머신(SVM) [시험출제 PART]
- 목적: 두 집단끼리 분류를 확실하게 하기 위해서, 마진을 최대화하는 결정선을 찾는 것이 목적이다.
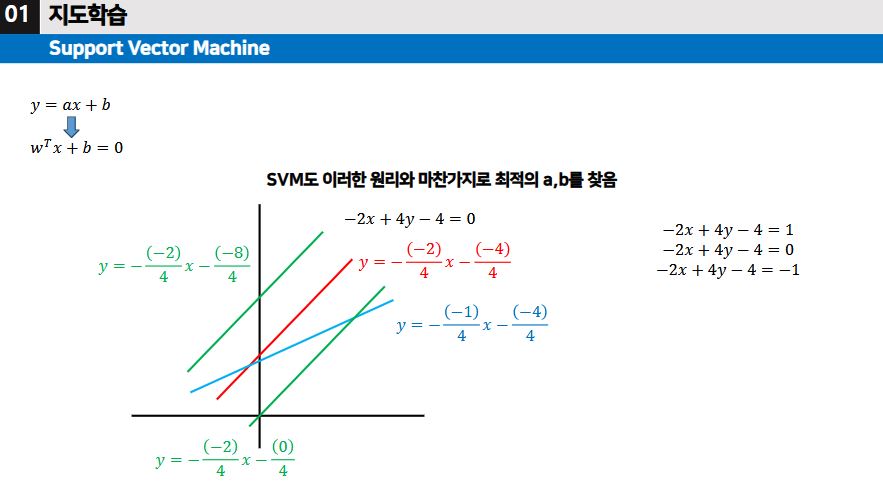
- 결정선은 wTx + b = 0 인데, wT에서 왜 전치를 시킬까? 그건 바로, 차원이 많아지면 계산이 어렵고 복잡해지기 때문에 복잡성을 낮추기 위하여 전치를 시킨 것이다.
- 두 집단을 분류하는 마진, 최적의 이동의 폭 λ 을 찾는 것이 핵심이다.

※ 참고) 벡터의 길이를 측정하는데 사용되는 함수로는, L2 norm 함수가 있다.

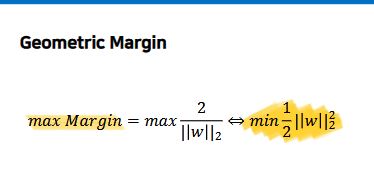

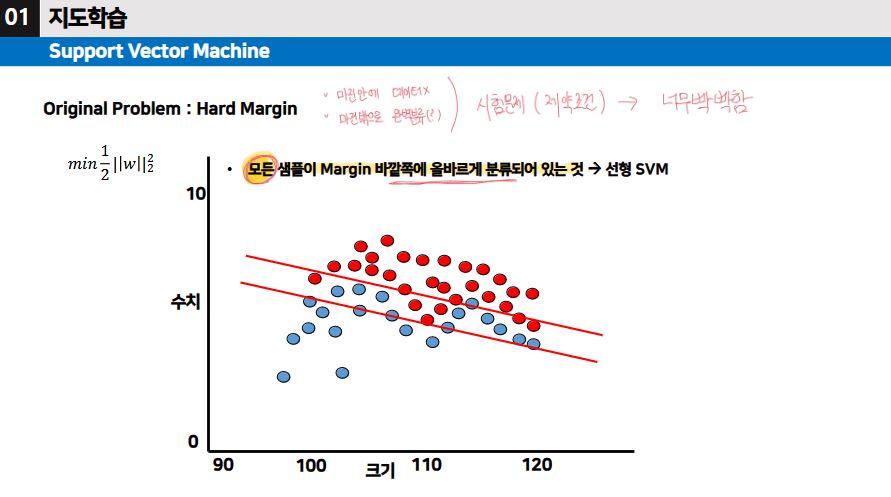
Hard Margin SVM [제약조건 → 시험출제]
- Hard Margin SVM은 모든 데이터가 결정 경계의 Margin 바깥쪽에 완벽하게 분리될 수 있다고 가정한다.
- 여기서, Margin이란, 결정 경계와 가장 가까운 데이터 사이의 거리를 말한다.
- 이 때, 결정 경계는 다음과 같은 목적을 달성하도록 학습된다.
- 마진을 최대화하면서 오류 없이 데이터를 완벽하게 분리하자.
- 제약 조건1) 마진 안에 데이터가 존재하면 안된다.
- 제약 조건2) 마진 밖으로 데이터를 두 집단으로 완벽 분류를 한다.
- Q&A) Hard Margin SVM이 선형 SVM인가?
- Hard Margin SVM은 선형적으로 데이터를 완벽히 분리할 수 있는 경우에 사용된다. 따라서 Hard Margin SVM은 선형 SVM의 한 종류라고 볼 수 있다. 모든 샘플이 Margin 바깥쪽에 올바르게 분류되어 있는 것 → 선형 SVM



하지만, Hard Margin SVM의 경우 제약 조건으로 인하여 너무 빡빡하다.

그래서 도입을 한 것이 Lagrangian Multiplier (마진을 최대화시키고, 가중치 업데이트를 하는 하이퍼 파라미터)이다.

※ 아래는 참고만 하자. 필기가 없거나 설명이 없다면 참고용








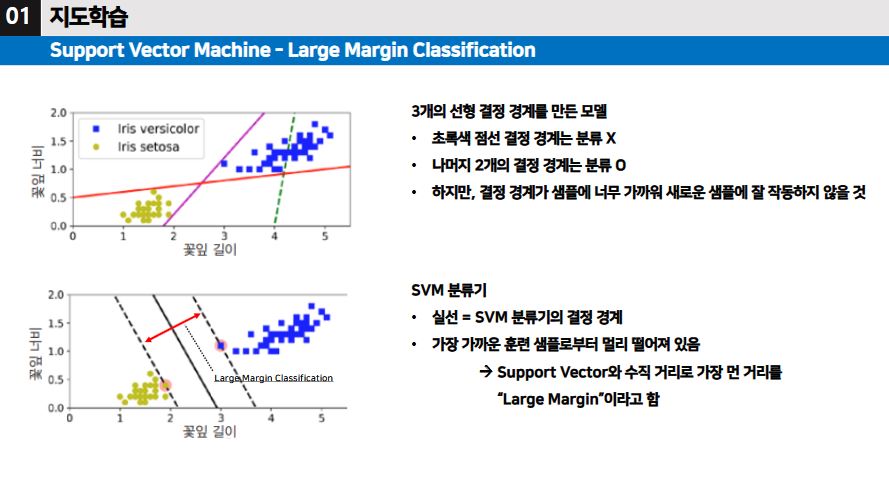
SVM 분류기
- Large Margin이란, 서포트벡터와 수직 거리로 가장 먼 거리를 말한다.

▶ SVM은 특성의 스케일에 민감하여, 스케일 조정을 하거나 정규화 과정을 거쳐야 분류기에 적합한 결정 경계를 설정한다

Hard Margin Classification의 문제점
- 이상치에 민감하다.
- 데이터가 선형적으로 구분될 수 있어야 제대로 작동한다.
- → 그래서 나온 것이 Soft Margin Classification 이다.
- Soft Margin Classification은 Hard Margin의 문제점을 해결하고, Margin 폭을 넓게 유지하는 것과 마진 오류 사이에 적절한 균형을 가진다.


Soft Margin Classification - Hyperparameter [시험 출제]
- 어느 정도의 오차는 이해하자.
- 크사이를 허용하자.
- 정규화된 파라미터 C값이 작을수록 마진의 범위가 커져 오차(에러)를 많이 허용한다.
※ 아래는 참고만 하자. 필기가 없거나 설명이 없다면 참고용



Soft Margin Classification : 마진 오류(오차)와 마진 폭을 넓게 유지해야 한다. (PPT 오류,, ㅎ ㅏ 교수님;)
- SVM 모델에서 Cost 하이퍼파라미터를 조절하여 Soft Margin 분류를 진행한다.
- C값이 낮은 경우, 마진이 좁아져 마진 오류는 적어졌지만 과소적합이 발생한다. (학습이 제대로 이루어지지 않음)
- C값이 큰 경우, 마진이 넓어져 마진 안에 샘플이 포함된다. 그래서 과대적합이 발생한다.
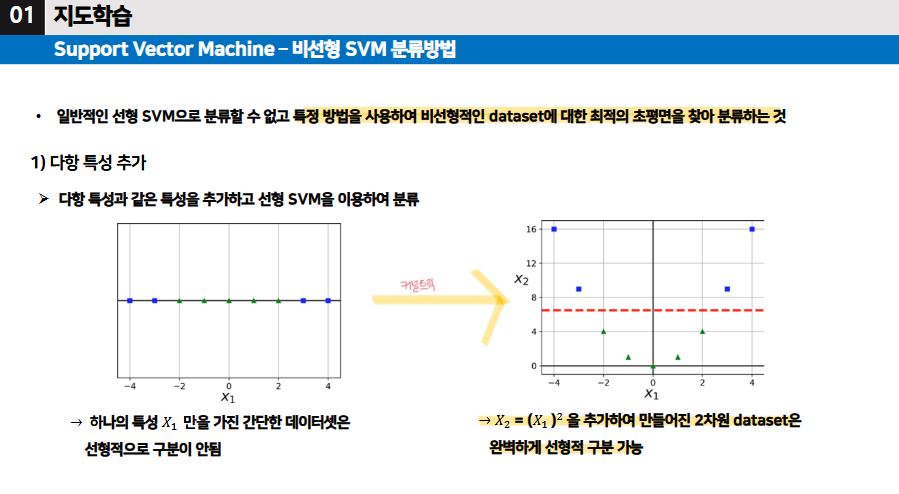


비선형 SVM 분류 방법
- 다항 특성 추가
- RBF 함수를 사용하여 유사도 특성
- 다항식 커널 : 커널 트릭을 사용 (실제로 특성을 추가X, 차원 수를 더 높은 차원으로 변형)

비선형 SVM 분류 방법 [여기가 핵심 - 시험 출제 PART]
- C값과 Gamma값에 대한 적절한 수치로 모델을 학습하는 것이 매우 중요하다.
- Cost는 SVM에서 오류를 얼마나 허용할 것인지를 조정하는 하이퍼 파라미터이다. 마진 크기와 오류 허용 간의 균형을 조절한다. Cost값을 올리면,
분류는 잘 못할 수도 있지만, 분류가 유연하다.마진을 줄이고, 오류를 최소화한다. - Gamma는 RBF 커널과 같은 비선형 커널에서 사용되며, 데이터 간의 유사도를 측정하는 파라미터이다. 결정 경계의 복잡도를 조절한다. Gamma값을 올리면 결정 경계가 복잡해지고 데이터가 가까운 것만 영향을 미친다 → 이 말이, 가까운 데이터(집단)끼리 뭉친다는 이야기같다. 추가로 데이터의 세부적인 패턴까지 학습하고, 훈련 데이터에서 높은 정확도를 보일 수 있지만, 결정 경계가 지나치게 복잡해져 과대적합이 일어날 수 있다.
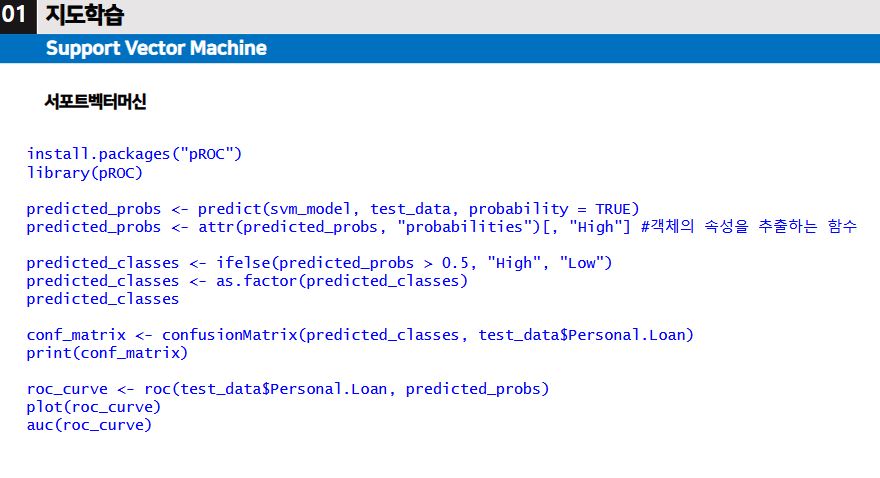
※ 실습은 아래에 다시 할 예정이다.


'머신러닝2 > 수업 필기' 카테고리의 다른 글
| 머신러닝2 14주차 (1) | 2024.12.11 |
|---|---|
| 머신러닝2 13주차 (0) | 2024.12.11 |
| 머신러닝2 11주차 (0) | 2024.12.11 |
| 머신러닝2 10주차 (0) | 2024.12.11 |
| 머신러닝2 7주차 (2) - 코드 부분 (0) | 2024.10.23 |