

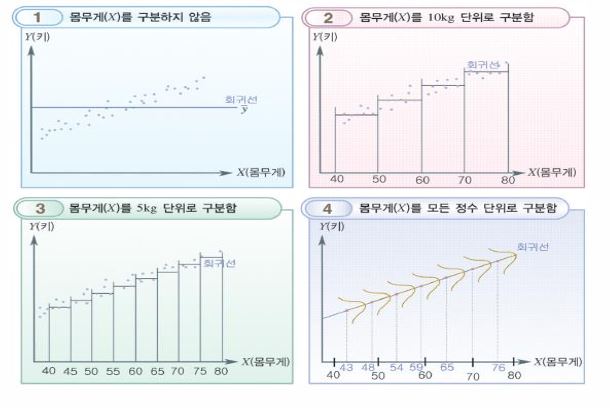
회귀분석
- 독립변수가 종속변수에 미치는 영향력의 크기를 파악하여 독립변수의 특정한 값에 대응하는 종속변수값을 예측하는 선형모형을 산출하는 방법
변수들(벡터)간의 관계 정도 → 모델링 - (결과) → 함수
모델링 → 수학적인 방법으로 → 회귀식

X - [ ] - Y
[ ] : 메커니즘 (모델)
모델링 하는 목적 : 원인(특성)들 특성을가지고 결과특성을 예측 및 설명
모델링의 의미
- 파라미터 값을 찾아내는 것
모델링의 의미
Y = a + b * X1 + c * X2
a, b, c : 파라미터 (매개변수)
→ 파라미터값을 찾아내는 것
input - [ ] - output : input데이터가 들어갔을 때 임계값에 도달해야만 output 데이터값이 나온다.
→ 이러한 관계를 형식화한 것이 모델이고 모델을 만드는 것을 모델링이라고 한다. == function


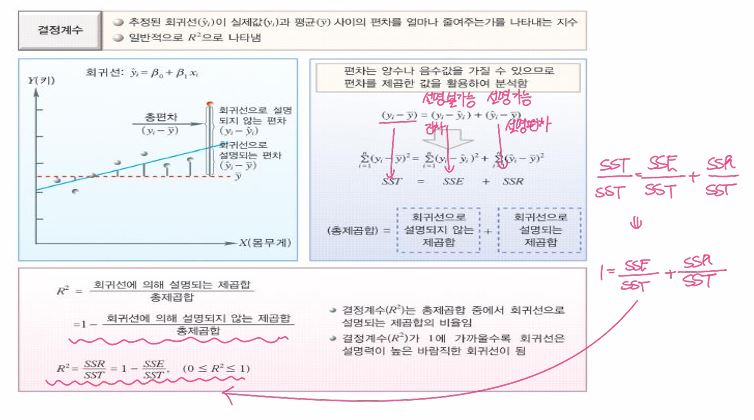

분산분석표 (ANOVA)
- 객관적으로 도출된 회귀식이 통계적으로 유의한가를 평가하는 방법 (검정)
회귀선으로 설명할 수 있는 편차 → 설명되는 부분
회귀선으로도 설명할 수 없는 편차(잔차) → 설명 안되는 부분
총 편차 = 회귀선으로 설명되지 않는 편차 + 회귀선으로 설명되는 편차
SST = SSE (잔차) + SSR (설명력)
분산분석표 (ANalysis Of VAriance = ANOVA분석, 분산분석)
- 객관적으로 도출된 회귀식이 통계적으로 유의한가를 평가하는 방법 (검정)
- 회귀선의 설명력(R^2)이 아무리 높아도 통계적으로 유의하지 않으면 일반화하여 사용하기 어려움
검정통계량 F0 = MSR/MSE (설명력 : 분산(산포), 잔차 : 분산(산포))
- H0 : R^2 = 0, 유의X
- H1 : R^2 != 0, 유의O
'머신러닝을 위한 통계학2 > 수업 필기' 카테고리의 다른 글
| 머신러닝을 위한 통계학2 11주차 (0) | 2024.12.08 |
|---|---|
| 머신러닝을 위한 통계학2 10주차 (0) | 2024.12.08 |
| 머신러닝을 위한 통계학2 5주차 (0) | 2024.10.28 |
| 머신러닝을 위한 통계학2 4주차 (0) | 2024.10.28 |
| 머신러닝을 위한 통계학2 3주차 (0) | 2024.10.28 |