표본공간과 사상
표본공간 : 확률실험을 실시하여 나타낼 수 있는 모든 결과의 집합
- 예시 : 주사위 한 개를 던지는 확률 실험에서의 표본공간은 S = {1, 2, 3, 4, 5, 6}
사상 : 표본공간을 구성하고 있는 원소 중에서 관심의 대상이 되는 원소들의 집합 (표본공간의 부분집합)
- 예시 : 주사위를 던지는 실험에서 “홀수가 나오는 사상”을 A 라고 하면 A = {1, 3, 5}
조건부 확률
확률 : 어떤 사상이 발생할 수 있는 가능성을 수치로 나타낸 것
조건부 확률 : 어떤 사상 B가 발생했다는 조건 하에서 또 다른 사상 A가 발생할 확률
- P(B|A) : 사건 A가 일어났을 때 B가 일어날 확률
- P(A∩B) : A와 B가 동시에 일어날 확률
expand.grid( ) : 주어진 벡터들로부터 가능한 모든 조합을 생성
nrow( ) : dataframe의 행의 수를 출력하는 함수
apply( ) : 행렬이나 배열에 조건을 적용시킬 때 사용하는 함수
▶ apply(함수, 1 또는 2, 적용할 함수)
subset( ) : 조건에 맞는 요소나 벡터 출력하는 함수
intersect( ) : 두 개의 벡터에서 공통된 요소를 출력 (A∩B)
▶ 교사상은 intersect() 함수를 이용해서 구할 수도 있다.
독립사상
- 사건 A와 사건 B가 서로에게 아무런 영향을 주지 않는다.
- 사상 B가 A에 영향을 주지 않으면 P(A|B) = P(A)
- 이 때 두 사상 A와 B는 서로 독립이라 한다.
- P(A) x P(F) = 0.18 ≠ P(A∩F)
- ★ P(A∩B) = P(A)P(B) 가 성립하지 않으므로 독립사상이 아니다.
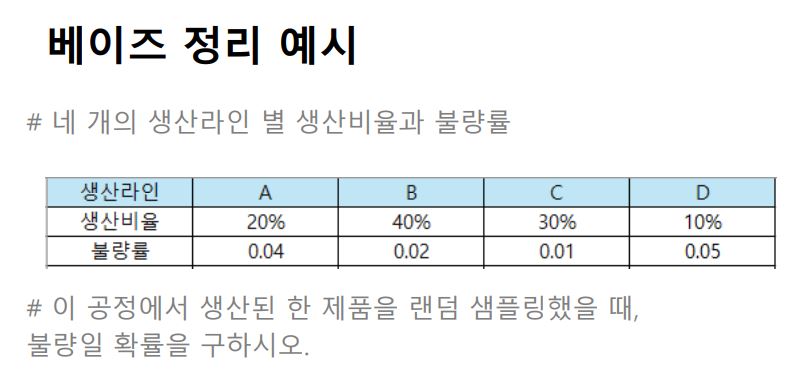
베이즈 정리
- 특정 사상 A가 관측되기 이전의 확률로부터 사상 A가 관측된 후의 조건부 확률을 구하기 위한 것
- 특정 사상 A가 관측되기 이전의 확률 P(B)는 사전확률
- 사상 A가 관측된 후의 조건부 확률 P(A|B)는 사후확률
- P(B|A): B가 발생했다는 조건 하에서 A의 확률 (우도, likelihood)
- P(B): 사건 B의 사전 확률, 어떤 사건이 발생하기 전에 이미 알고 있는 확률 (evidence)

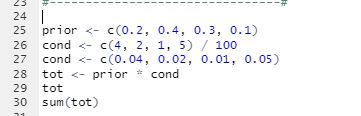





[ 시험 출제 가능성 ]




※ 베이즈 정리로 구한 사후확률의 합은 1이 된다!
+ 사상 A와 D의 사후 확률은 늘어났지만, 사상 B와 C의 사후확률은 줄어들었다. 이는 생산라인 A와 D의 불량률이 상대적으로 높았고, 생산라인 B와 C의 불량률은 상대적으로 낮았기 때문이다.
'머신러닝을 위한 통계학1 > R언어 실습' 카테고리의 다른 글
| 통계학 R언어 [도수분포표 그리는 방법 (참고)] (0) | 2024.04.21 |
|---|---|
| 통계학 R언어 실습 (7) (2) | 2024.04.19 |
| 통계학 R언어 실습 (5) (1) | 2024.04.18 |
| 통계학 R언어 실습 (4) (1) | 2024.04.18 |
| 통계학 R언어 실습 (3) (1) | 2024.04.18 |