이산수학 중간고사 시험 설명
- 단답형 : 정의 문제, 값을 쓰시오, 결과값 출력, 예시) 진수 및 보수 문제
- 서술형 : 증명 문제, 논리 문제
Chapter 01. 수의 표현과 연산
- 1.1 수의 체계
- 1.2 수의 연산
- 1.3 진법별 표현
- 1.4 진법 간 변환
- 1.5 진법별 사칙연산
- 1.6 컴퓨터에서의 수의 표현과 연산
이 단원을 왜 배우는가 ?
- 현재, 지능 정보 기술을 적극적으로 활용하는 4차 산업혁명 시대가 도래하였다. 4차 산업혁명 시대에는 인공지능, 빅데이터, 클라우드 컴퓨팅과 같은 지능화 기술이 가장 핵심적인 주제가 되고 있다. 이 지능화 기술은 숫자, 문자, 그림, 음악 등 다양한 형태로 데이터를 표현하고 처리하는 인간의 방식과 달리 컴퓨터, 인터넷 기술처럼 0과 1만을 이용해 모든 데이터를 표현하고 처리하는 디지털 방식을 이용한다.
- 데이터를 어떻게 디지털 방식으로 연산하고 표현하는지 이해하고, 수를 정수 데이터로 변환하기 위해 일반적인 수의 체계와 연산 및 표현을 알아본다. 그리고 우리가 사용하는 다양한 데이터를 컴퓨터가 어떻게 표현하고 연산하는지 살펴본다.
1.1 수의 체계

옛날 사고 방식으로 수는 정수와 그 비율로 보았다. 지금의 수는 자연수 1에서 시작하여 1씩 증가하는 수라는 개념에서 시작하여 음수의 개념까지 확장하여 음의 정수, 0, 양의 정수 (자연수) 로 분리되는 정수의 개념이 도입되었다. 그 이후 연속적인 수라는 개념이 도입되면서 분수 B/A (A, B : 정수, A != 0)의 개념을 담고 있는 유리수와 그 이후 무리수, 실수, 허수, 복소수가 나왔다.
기수 : 10진수, 2진수와 같이 수 표현의 근거를 알려주는 수, 숫자 끝에 아래첨자로 표기
예) 𝟏𝟒𝟑𝟏𝟎(10), 𝟏𝟏𝟎𝟎𝟏𝟐(2), ...
순환 : 나누었을 때 나머지가 똑같다.
무한 : 나누기 평생 (나누기 나머지는 나누는 수보다 작다.)
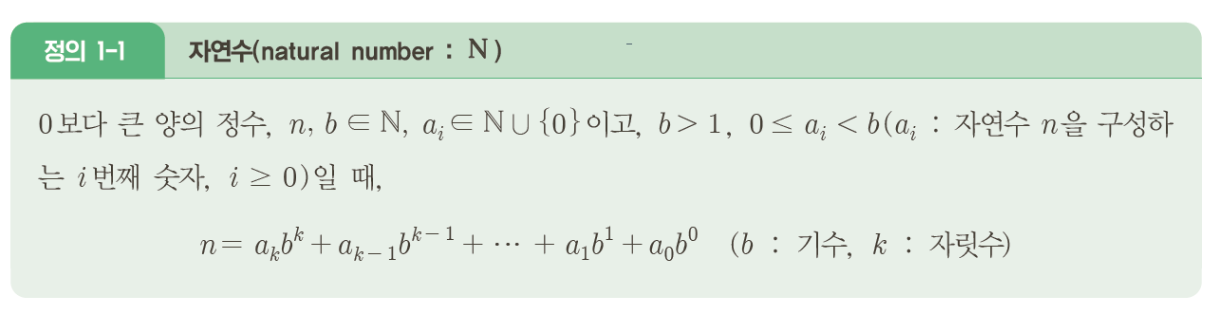

- 0 : 양의 정수나 음의 정수에 속하지 않는 수, +나 –와 같은 부호가 붙지 않는다.
- 음의 정수 : 숫자 앞에 - 부호가 붙거나 부호가 생략된 0보다 작은 수
- 양의 정수 : 숫자 앞에 + 부호가 붙거나 부호가 생략된 0보다 큰 수, 자연수와 같은 범위의 수
- 양의 정수 = 자연수

([정의 문제] 시험출제 가능성)
★ 2/9, 1/2 : 하한항으로 구성
유리수의 특징
- 정수 집합도 포함 Q > Z
- 유리수는 같은 값을 다르게 표현할 수 있다.

무리수 특징
- R > Q + I, 유리수 집합과 무리수 집합은 모두 실수 집합에 포함된다.
- 실수는 분수형태로 표현할 수 있으면 유리수, 그렇지 않으면 무리수로 구분한다.
- 유리수 : 유한하게 나열 OR 규칙성을 갖고 무한히 나열되는 형태
- 무리수 : 소수부의 숫자가 규칙성 없이 무한히 나열되어 분수로 표현X



실수와 허수를 합치면 복소수이다. 허수는 간단히 말하여, 제곱하여 음수가 되며 제곱했을 때 0보다 작은 값이 되는 가상의 수이다.

1.2 수의 연산
수를 연산한 결과는 수의 체계와 연산자의 종류에 따라 결정된다. 연산에 피연산자로 사용한 수, 그리고 연산 결과로 나오는 수의 체계와 연산자의 관계는 닫힘 성질로 정의할 수 있다.

[시험 출제 유형, 표 채우는 유형]
- 자연수의 경우 : 2 - 4 = 자연수X, 3 / 2 = 자연수 X
- 정수의 경우 : 3 / 2 = 정수X
- 무리수는 전부 안 된다.

합과 곱에 대해서는 항등원과 역원이 존재한다.

항등원 : 임의의 수 a와 연산했을 때 결과가 그대로 a가 나오게 만드는 수

역원 : 어떤 수 a와 연산했을 때 항등원이 나오게 만드는 수


※ 시험 때 i가 어디서 (위치 확인)부터 시작하는지 잘 확인하자!!



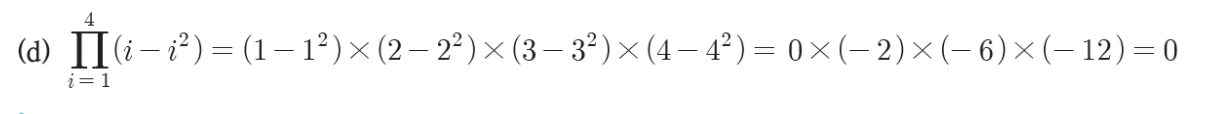

팩토리얼 연산에 사용되는 수는 1보다 크거나 같은 자연수이지만, 연산식에 따라 0!을 계산할 수 있도록 0!을 1로 정의한다.


수를 나누면 몫(quotient) 과 나머지(remainder)를 구할 수 있다.
★ 나누어 떨어진다는 말은 다시 말하면, '배수이다' 라는 표현과 같다.
▶ d는 m의 약수이다, m은 d의 배수에 포함된다.


- [1점짜리 유형으로 나올 가능성 높다!]
- 몫을 구하는 연산 : div
- 나머지를 구하는 연산 : mod
1.3 진법별 표현
- 수 : '양'을 뜻함
- 숫자 : 수를 표현하는 글자

몇 개의 숫자를 이용하여 수를 표현하느냐에 따라 진법이 결정된다. 현재 사용하고 있는 진법의 표기를 기수(base)라고 한다.
컴퓨터의 발전으로 인해 컴퓨터에서 표현하고 연산해야 하는 데이터의 종류가 다양해지고 그에 따라 데이터의 크기도 커지면서 2진법만을 이용하여 모든 데이터를 표현하기에는 표현 길이가 너무 길어졌다. 그래서 컴퓨터에서는 길어진 데이터 표현을 간략하게 만들어 효율적으로 활용하기 위해 8진수와 16진수를 사용하게 되었기 때문이다.
n진법 : 수의 한자리를 n개의 숫자로 표현


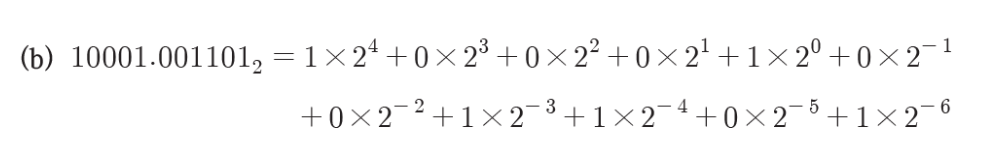

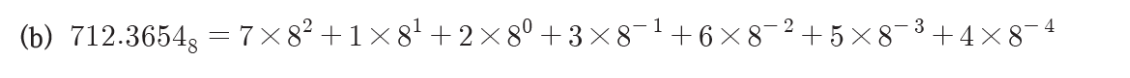


16진수 : 0부터 15까지의 숫자를 이용하여 표현한 수
1.4 진법 간 변환

※ 10진수와 2진수는 어떤 진법으로든 변환이 가능하지만, 8진수와 16진수는 서로 직접 변환이 불가능하다!!!
그러므로, 8진수를 16진수로, 또는 16진수를 8진수로 변환하기 위해서는 먼저 10진수나 2진수로 변환한 후에 8진수나 16진수로 변환해야 한다.



[이 이후 시험 출제 가능성 매우 높음]
2진수, 8진수, 16진수를 각각의 기수와 자릿수로 표현한 식을 계산하면 10진수로 변환된다.

2진수를 8진수/16진수로 변환하거나 8진수/16진수를 2진수로 변환하는 방법은 먼저 10진수로 변환한 다음 다른 진수로 변환하는 것이다. 또는 비트 단위로 나누어 변환하는 것이다.

- ★ 8진수를 구성하는 각 자리의 숫자를 3비트로 구성된 2진수로 표현하면 8진수를 2진수로 변환할 수 있다.
- 반대로 2진수를 8진수로 변환할 때는 2진수를 소수점 기준으로 3비트씩 한 단위로 묶고 각 단위를 10진수로 표현하여 8진수로 변환한다.


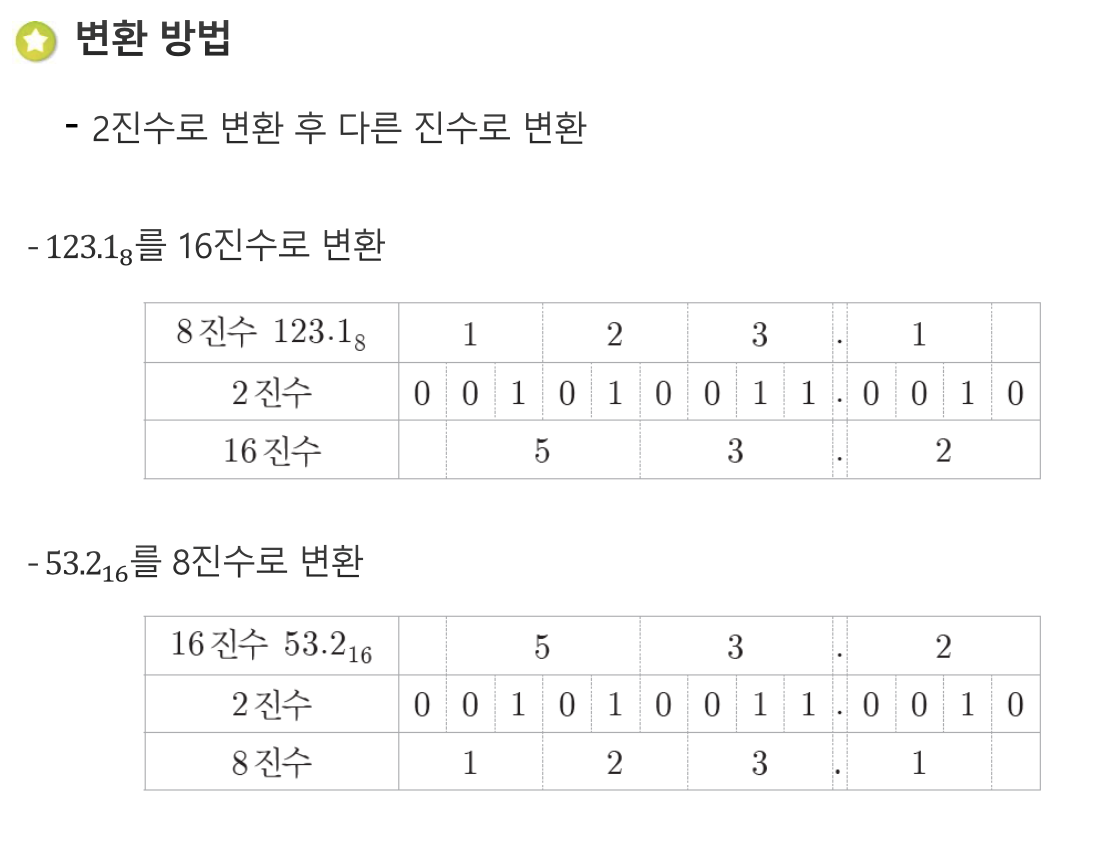
8진수와 16진수간의 직접적인 변환은 불가능하다. 10진수 또는 2진수로의 변환을 거쳐야 변환이 가능하다.
※ 변환에 있어서 0을 함부로 생략하지 말자!!!
